
To construct a tangent to a circle of radius 4 cm from a point on the concentric circle of
radius 6 cm.
Answer
620.1k+ views
Hint: For solving this problem, we should be aware about the concept of tangents. Basically, a tangent to the curve is a straight line that touches a curve but does not cross it. In addition, it is important to know the basics of construction to find the tangent line.
Complete step-by-step answer:
To construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm,
we follow few basic steps,
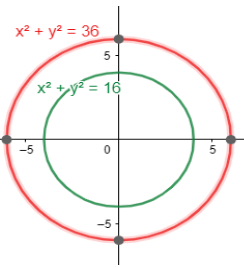
Step 1: We first draw two concentric circles of radius 4 cm and 6 cm respectively (Both the circles
should have the same center).
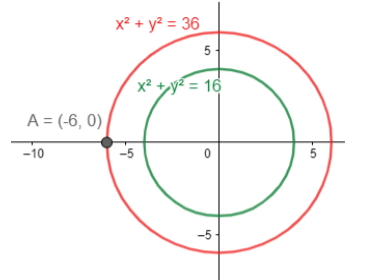
Step 2: We now mark a point A on the larger circle from where we could draw a tangent to the smaller circle. Thus, we have
 ,
,
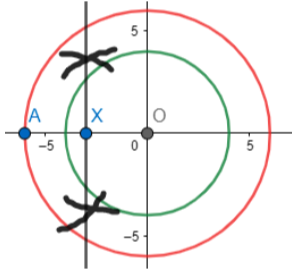
Step 3: We join A to the center of the circle (O) and then make a perpendicular bisector of this line segment AO. We do this by taking a compass and taking length in it about more than half the distance between PO. Then make two arcs above and below AO from points A and O as shown. Now,we join the line made of arc intersections.
Step 4: Now, we draw the circle with XO as radius and center as X. Thus, we get the figure below. We mark the points of intersections as points B and C.
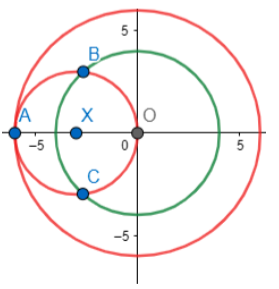
Step 5: We join line AB and AC. These are the required tangents. Thus, we have,
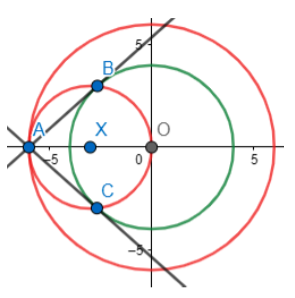
Hence, AB and AC are the required tangents.
Note: While constructing the tangents, we come across a step where we have to make a perpendicular bisector. Thus, while solving questions about construction, it is important to be aware that although arcs can be drawn on one side of the line (we refer to line AO in this case) to make a perpendicular bisector. We make arcs on both sides of the line AO (as seen two arcs have been made on both sides of line AO), since this makes it easier while construction on the paper while doing it with hand. Further, one can choose any other point on the larger circle and use a similar method to get tangents from that point.
Complete step-by-step answer:
To construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm,
we follow few basic steps,
Step 1: We first draw two concentric circles of radius 4 cm and 6 cm respectively (Both the circles
should have the same center).

Step 2: We now mark a point A on the larger circle from where we could draw a tangent to the smaller circle. Thus, we have

Step 3: We join A to the center of the circle (O) and then make a perpendicular bisector of this line segment AO. We do this by taking a compass and taking length in it about more than half the distance between PO. Then make two arcs above and below AO from points A and O as shown. Now,we join the line made of arc intersections.

Step 4: Now, we draw the circle with XO as radius and center as X. Thus, we get the figure below. We mark the points of intersections as points B and C.

Step 5: We join line AB and AC. These are the required tangents. Thus, we have,

Hence, AB and AC are the required tangents.
Note: While constructing the tangents, we come across a step where we have to make a perpendicular bisector. Thus, while solving questions about construction, it is important to be aware that although arcs can be drawn on one side of the line (we refer to line AO in this case) to make a perpendicular bisector. We make arcs on both sides of the line AO (as seen two arcs have been made on both sides of line AO), since this makes it easier while construction on the paper while doing it with hand. Further, one can choose any other point on the larger circle and use a similar method to get tangents from that point.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




