Question

Three girls Reshma, Salma, and Mandip are playing a game by standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma and Mandip, and Mandip to Reshma. If the distance between Reshma and Salma, and Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip?

Answer 1

Hint:
Here, we need to find the distance between Reshma and Mandip. We will use congruence to prove that the radius from the centre of the circle to Reshma, bisects the distance between Reshma and Mandip. Then, we will use Pythagoras’s theorems to find the value of half the distance between Reshma and Mandip, and double it to get the distance between Reshma and Mandip.

Formula Used:
We will use the following formulas:
1) The Pythagoras’s theorem states that the square of the hypotenuse of a right angled triangle is equal to the sum of squares of the other two sides, that is \[{\rm{Hypotenuse}}{{\rm{e}}^2} = {\rm{Bas}}{{\rm{e}}^2} + {\rm{Perpendicula}}{{\rm{r}}^2}\].
2) The square of the difference of two numbers \[a\] and \[b\] is given by the algebraic identity \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\].

Complete step by step solution:

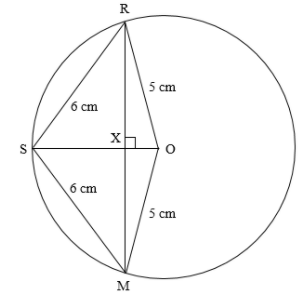
Here, R, S, and M are the points on the circle with centre O, where Reshma, Salma, and Mandip are standing. The distance between Reshma and Salma is \[RS = 6\] cm. The distance between Salma and Mandip is \[SM = 6\] cm.
We need to find the distance between Reshma and Mandip, that is \[RM\].
We can observe that OR, OS, and OM are the radii of the circle.
Thus, we get
\[OR = OS = OM = 5\]cm
Let \[OX = x\] cm.
Thus, we get
\[\begin{array}{l} \Rightarrow SX + OX = OS\\ \Rightarrow SX + x = 5\\ \Rightarrow SX = 5 - x\end{array}\]
Now, we will use congruence of triangles.
Now, in triangles ORS and OMS, we can observe that
\[OR = OM\] (Radii of the same circle)
\[RS = MS = 6\]cm (Given)
\[OS = OS\] (Common side)
Therefore, by S.S.S. congruence criterion, we have proved that the triangles ORS and OMS are congruent.
Since corresponding parts of congruent triangles are equal, we get \[\angle ROS = \angle MOS\].
Since \[\angle ROS = \angle MOS\], we get \[\angle ROX = \angle MOX\].
Now, in triangles ORX and OMX, we can observe that
\[OR = OM\] (Radii of the same circle)
\[\angle ROX = \angle MOX\] (Since \[\angle ROS = \angle MOS\])
\[OX = OX\] (Common side)
Therefore, by S.A.S. congruence criterion, we have proved that the triangles ORX and OMX are congruent.
Since corresponding parts of congruent triangles are equal, we get \[RX = MX\].
Since \[\angle ROS = \angle MOS\], the point \[X\] is the midpoint of \[RM\].
Thus, \[OX\] bisects \[RM\].
This means that the radius \[OS\] also bisects the chord \[RM\].
We know that if a radius bisects a chord, then the radius is perpendicular to the chord.
Therefore, we get
\[\angle OXR = \angle OXM = 90^\circ \]
Therefore, the triangles ORX and SRX are right angled triangles.
Now, we will use Pythagoras's theorem in triangles ORX and SRX.
The Pythagoras’s theorem states that the square of the hypotenuse of a right angled triangle is equal to the sum of squares of the other two sides, that is \[{\rm{Hypotenuse}}{{\rm{e}}^2} = {\rm{Bas}}{{\rm{e}}^2} + {\rm{Perpendicula}}{{\rm{r}}^2}\].
Therefore, in triangle ORX, we get
\[O{R^2} = R{X^2} + O{X^2}\]
Substituting \[OR = 5\] cm and \[OX = x\] cm in the equation, we get
\[ \Rightarrow {5^2} = R{X^2} + {x^2}\]
Simplifying the expression, we get
\[ \Rightarrow 25 = R{X^2} + {x^2}\]
Subtracting \[{x^2}\] from both sides, we get
\[ \Rightarrow 25 - {x^2} = R{X^2}\]
Using Pythagoras’s theorem in triangle SRX, we get
\[S{R^2} = R{X^2} + S{X^2}\]
Substituting \[SR = 6\]cm, \[R{X^2} = 25 - {x^2}\]cm and \[SX = \left( {5 - x} \right)\] cm in the equation, we get
\[ \Rightarrow {6^2} = 25 - {x^2} + {\left( {5 - x} \right)^2}\]
Using the algebraic identity \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\], we get
\[ \Rightarrow {6^2} = 25 - {x^2} + 25 + {x^2} - 10x\]
Simplifying the expression, we get
\[ \Rightarrow 36 = 50 - 10x\]
Rewriting the expression, we get
\[ \Rightarrow 10x = 50 - 36\]
Subtracting the terms, we get
\[ \Rightarrow 10x = 14\]
Dividing both sides by 10, we get
\[ \Rightarrow x = 1.4\]
Substituting \[x = 1.4\] in the equation \[R{X^2} = 25 - {x^2}\], we get
\[ \Rightarrow R{X^2} = 25 - {\left( {1.4} \right)^2}\]
Simplifying the expression, we get
\[\begin{array}{l} \Rightarrow R{X^2} = 25 - 1.96\\ \Rightarrow R{X^2} = 23.04\end{array}\]
Taking the square root on both the sides, we get
\[ \Rightarrow RX = 4.8\]
Therefore, we get
\[RX = MX = 4.8\] cm
Now, we can observe that \[RM\] is the sum of \[RX\] and \[MX\].
Therefore, using \[RX = MX = 4.8\]cm, we get
\[\begin{array}{l} \Rightarrow RM = RX + MX\\ \Rightarrow RM = 4.8 + 4.8\\ \Rightarrow RM = 9.6\end{array}\]

Therefore, we get the distance between Reshma and Mandip as \[9.6\] cm.

Note:
We used the S.S.S. and S.A.S. congruence criterion in the solution.
According to the S.S.S. congruence criterion, if the corresponding sides of two triangles are equal, then the two triangles are congruent.
According to the S.A.S. congruence criterion, if two corresponding sides of two triangles are equal, and the corresponding angle formed by those sides is also equal, then the two triangles are congruent.