Question

Three electric bulbs of \[200\,W\],$200\,W$ and $400\,W$ are shown in figure. The resultant power of the combination

A. $800\,W$
B. $400\,W$
C. $200\,W$
D. $600\,W$

Answer 1

Hint: Power is the rate of change of work done per unit time. When a bulb is connected with the battery it dissipates the electrical energy into light energy and heat So when we calculate the power it means how much energy dissipated by the bulb per second.

Complete step by step answer:
In this combination three electric bulbs have power ${{P}_{1}},{{P}_{2}}\And {{P}_{3}}$ where ${{P}_{1}}=200W$, ${{P}_{2}}=200W$, ${{P}_{3}}=400W$. In this arrangement ${{P}_{1}}$ and ${{P}_{2}}$ are connected in parallel but ${{P}_{3}}$ is connected in series with resultant of ${{P}_{1}}$ and ${{P}_{2}}$. We have to use the formula of power
$P=\dfrac{{{V}^{2}}}{R}$
Then, $R=\dfrac{{{V}^{2}}}{P}$
${{R}_{1}}=\dfrac{{{V}^{2}}}{{{P}_{1}}}$
$\Rightarrow {{R}_{2}}=\dfrac{{{V}^{2}}}{{{P}_{2}}}$
When the resistor connected in series then we have a formula of equivalent resistance
${{R}_{eq}}={{R}_{1}}+{{R}_{2}}$
Where, ${{R}_{1}}\And {{R}_{2}}$ is the resistance connected in series.
$\dfrac{{{V}^{2}}}{{{P}_{eq}}}=\dfrac{{{V}^{2}}}{{{P}_{1}}}+\dfrac{{{V}^{2}}}{{{P}_{2}}}$
Dividing both side by ${{V}^{2}}$, we get ${{P}_{eq}}$ of series combination
$\dfrac{1}{{{P}_{eq}}}=\dfrac{1}{{{P}_{1}}}+\dfrac{1}{{{P}_{2}}}$

When the resistor connected in parallel then then we have a formula of equivalent resistance
\[\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}\]
Where, ${{R}_{1}}\And {{R}_{2}}$ is the resistance connected in parallel.
After putting the value of ${{R}_{1}}\And {{R}_{2}}$in above equation, we get
$\dfrac{{{P}_{eq}}}{{{V}^{2}}}=\dfrac{{{P}_{1}}}{{{V}^{2}}}+\dfrac{{{P}_{2}}}{{{V}^{2}}}$
After multiplying both side by ${{V}^{2}}$, we get ${{P}_{eq}}$ of parallel combination
\[{{P}_{eq}}={{P}_{1}}+{{P}_{2}}\]
In this problem power ${{P}_{1}}\And {{P}_{2}}$ are connected in parallel then resultant power of ${{P}_{1}}\And {{P}_{2}}$ is

${{P}_{eq}}={{P}_{1}}+{{P}_{2}}$
$\Rightarrow {{P}_{eq}}=200+200$
$\Rightarrow {{P}_{eq}}=400\,W$
But ${{P}_{3}}$ connected in series through ${{P}_{1}}\And {{P}_{2}}$ then resultant power of ${{P}_{1}},{{P}_{2}}\And {{P}_{3}}$

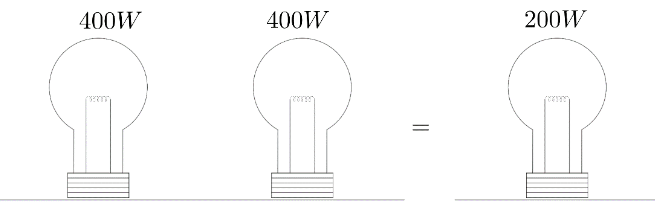
$\Rightarrow {{P}_{eq}}=\dfrac{1}{400}+\dfrac{1}{{{P}_{3}}}$
$\Rightarrow {{P}_{eq}}=\dfrac{1}{400}+\dfrac{1}{400}$
$\therefore {{P}_{eq}}=200\,W$
Hence, the resultant power of the combination is 200 W.

Hence, the correct answer is option C.

Note: Electric bulb converts the electrical energy into light energy and heat energy. In the series combination of resistor current is constant but in the case of parallel combination voltage is constant. Equivalent power means when we remove all three bulbs and connect a single bulb having the same resistance then power of a single bulb is equal to the equivalent power of three bulbs.