Question

There are $72$ students in the class.

From the figure:
(i) How many students in the class prefer cricket?
(ii) How many students in the class prefer basketball?
(iii) How many students in the class prefer a sport other than cricket, hockey, basketball or athletics?

Answer 1

Hint: When the angles of each section are given, as well as the total number of students we make use of the unitary method to find the required values. The angle formed by a complete circle is established to be ${360^ \circ }$. Since each angle with respect to the total number of students for the respective sport is provided we need to find the relationship in terms of number of students.

Complete step-by-step answer:
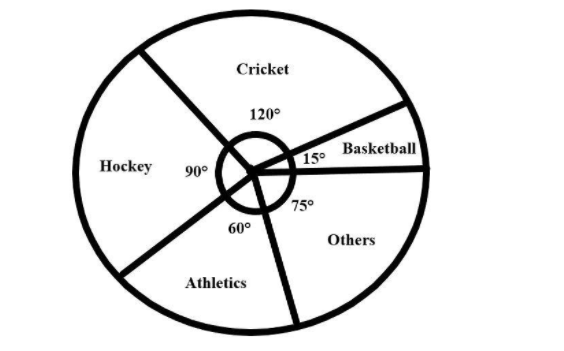
We are given a diagram that provides an angle for each sport which represents the portion of the class that has chosen the respective sport. A total of $72$ students make up the class in consideration.
Our task is that: we need to associate the value of each angle to the number of students in each sport, so that we can find the required values asked in the question.
Remember that since every circle has the complete angle as ${360^ \circ }$, and the total number of students represented within the circle is $72$, their relationship can be expressed as:
$ \Rightarrow 72\;students = {360^ \circ }$
So by unitary method we can say that $1$ student occupies a degree of:
$ \Rightarrow 1\;student = {\left( {\dfrac{{360}}{{72}}} \right)^ \circ }$
$ \Rightarrow 1\;student = {5^ \circ }$
So for the number of students that prefers a particular sport say ‘x’, the formula will be:
$ \Rightarrow Number\;of\;students\;in\,'x' = \dfrac{{Angle\;of\;all\;students\;opting\;sport\;'x'}}{{Angle\;of\;1\;student}}$
So now we can proceed to the required subdivisions.
(i) The number of students that have chosen cricket as their preference can be denoted as ‘C’.
We know that the angle that represents the portion of students of the class that prefer cricket is ${120^ \circ }$.
Then the number of students that will prefer cricket is can be expressed as:
$ \Rightarrow C = \dfrac{{{{120}^ \circ }}}{{{5^ \circ }}}$
$ \Rightarrow C = 24$ students
(ii) The number of students that have chosen basketball as their preference can be denoted as ‘B’.
We know that the angle which represents the portion of students of the class that prefer basketball is ${15^ \circ }$.
Then the number of students that will prefer cricket is can be expressed as:
$ \Rightarrow B = \dfrac{{{{15}^ \circ }}}{{{5^ \circ }}}$
$ \Rightarrow B = 3$ students
(iii) The number of students that have chosen other sports as their preference can be denoted as ‘O’.
We know that the angle that represents the portion of students of the class that prefer other sports is ${75^ \circ }$.
Then the number of students that will prefer cricket is can be expressed as:
$ \Rightarrow O = \dfrac{{{{75}^ \circ }}}{{{5^ \circ }}}$
$ \Rightarrow O = 15$ students
Therefore:
(i) Number of students in the class who prefer cricket is $24$.
(ii) Number of students in the class who prefer basketball is $3$.
(iii) Number of students in the class who prefer a sport other than cricket, hockey, basketball or athletics is $15$.

Note: In circles there is an important concept we need to remember, that is a sector of a circle. The sector is essentially a subset of a circle that can be identified by the three items defined as: A circular sector is a region on the circle bounded by one arc and two radii. Such a region comes in two forms: the Minor sector and the Major sector.