Question

The volume of a right circular cone is $9856c{m^3}$. If the diameter of the base is 28 cm, find
(i). Height of the cone
(ii). The slant height of the cone
(iii). Curved surface area of the cone

Answer 1

Hint: To attempt this question prior knowledge of right circular cone and its formula is must and also remember to use these formulas of right circular cone \[\text{Volume} = \dfrac{1}{3}\pi {\left( {\text{radius}} \right)^2}\left( {\text{height}} \right)\], \[\text{Slant height(l)} = \sqrt {{{\left( {\text{radius}} \right)}^2} + {{\left( {\text{height}} \right)}^2}} \] and $\text{Curved Surface Area} = \pi rl$, use this information to approach the solution.

Complete step-by-step solution:

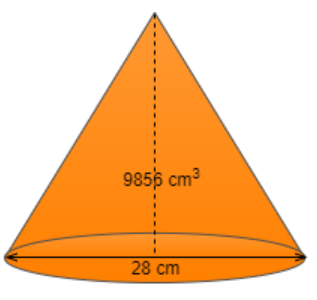
It is given in the question that the volume of the right circular cone is $9856c{m^3}$ whose diameter of the base is 28 cm
(i) Height of the cone
As we know that volume of right circular cone is given as; \[Volume = \dfrac{1}{3}\pi {\left( {\text{radius}} \right)^2}\left( {\text{height}} \right)\]
Also, we know that $\text{Radius} = \dfrac{\text{diameter}}{2}$
Therefore, radius of the right circular cone =$\dfrac{{28}}{2} = 14cm$
Now substituting the values in the formula of volume of right circular cone we get
\[9856 = \dfrac{1}{3}\dfrac{{22}}{7}{\left( {14} \right)^2}h\]
$ \Rightarrow $\[h = \dfrac{{9856 \times 21}}{{196 \times 22}}\]
So, Height (h) = 48 cm.

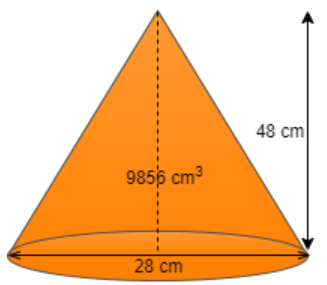
(ii) Slant height of the cone
We know that formula of slant height is given as; \[\text{Slant height(l)} = \sqrt {{{\left( {\text{radius}} \right)}^2} + {{\left( {\text{height}} \right)}^2}} \]
Substituting the values in the formula of slant height we get
\[\text{Slant height(l)} = \sqrt {{{\left( {14} \right)}^2} + {{\left( {48} \right)}^2}} \]
$ \Rightarrow $\[\text{Slant height(l)} = \sqrt {196 + 2304} \]
So, Slant height = 50 cm.

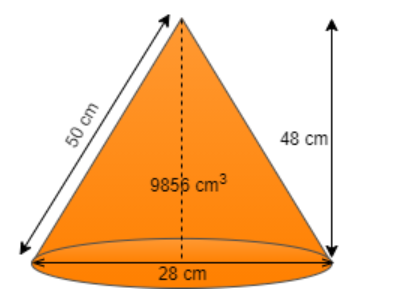
(iii) Curved surface area of the cone
We know that curved surface area of right circular cone is given as; $\text{Curved Surface Area} = \pi rl$ here r is the radius and l is the slant height
Substituting the values of r and l in the above formula we get
$\text{Curved Surface Area} = \dfrac{{22}}{7} \times 14 \times 50$
$ \Rightarrow \text{Curved Surface Area} = 22004c{m^2}$
Therefore, the curved surface area of the right circular cone is $22004c{m^2}$.

Note: In the above solution we came across the term “right circular cone” which is a three-dimensional shape which is also one of the types of a cone but the properties which make it different from the other cones are that its axis is always perpendicular to the plane of circular base’s center and due to which it makes a right angle at the base of the cone.