Question

The vertices of a $\Delta GHK$ having coordinates $G\left( -3,4 \right)$, $H\left( 1,-3 \right)\And K\left( 2,7 \right)$ then find the equation of an altitude which is passing through the vertex G and resting on the side HK.
(a)$10x+y=-26$
(b)$10x+y=7$
(c)$10x+y=27$
(d)$x+10y=37$

Answer 1

Hint: First of all draw a $\Delta GHK$ with vertices $G\left( -3,4 \right)$, $H\left( 1,-3 \right)\And K\left( 2,7 \right)$ then we are going to find the equation of an altitude passing through G. We know that the equation of a line consists of a slope and the y-intercept and the general form of the equation of a line is $y=mx+c$. The altitude is making a right angle with the side it rests on and we know that if two lines are perpendicular to each other then the relation between their slopes is ${{m}_{1}}\left( {{m}_{2}} \right)=-1$. So, find the slope of the side HK and substitute this slope value in ${{m}_{1}}\left( {{m}_{2}} \right)=-1$ we will get the slope for the altitude. Now, substitute this value of slope in $y=mx+c$, and also this altitude is passing through the point G so satisfy the coordinates of G in $y=mx+c$ and which will eventually give you the equation of an altitude.

Complete step-by-step solution:
In the below diagram, we have shown a $\Delta GHK$ with vertices $G\left( -3,4 \right)$, $H\left( 1,-3 \right)\And K\left( 2,7 \right)$.
 

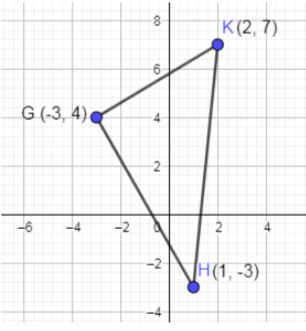
We are asked to find the altitude of this triangle which is passing through point G and is resting upon the side HK.
In the below figure, we have shown an altitude GB on the side HK of the triangle.

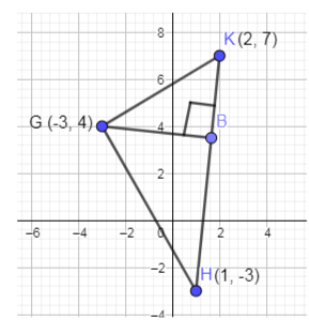
We know that altitude is making right angles with the side it rests upon. This means that GB and HK are perpendicular to each other in $\Delta GHK$. The relation between slopes of two lines which are perpendicular to each other is equal to:
${{m}_{1}}\left( {{m}_{2}} \right)=-1$……. Eq. (1)
Let us suppose that ${{m}_{1}}$ is the slope of side HK and ${{m}_{2}}$ is the slope of altitude.
We are going to find the slope of side HK with coordinates of H and K as $H\left( 1,-3 \right)\And K\left( 2,7 \right)$.
The slope calculations for two points say $P\left( {{x}_{1}},{{y}_{1}} \right)\And Q\left( {{x}_{2}},{{y}_{2}} \right)$ is given as:
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Using this slope calculation we can calculate the slope of side HK as:
$\begin{align}
  & {{m}_{1}}=\dfrac{7-\left( -3 \right)}{2-1} \\
 & \Rightarrow {{m}_{1}}=\dfrac{7+3}{2-1} \\
 & \Rightarrow {{m}_{1}}=\dfrac{10}{1} \\
\end{align}$
Substituting the above value of slope in eq. (1) we get,
$\begin{align}
  & {{m}_{1}}\left( {{m}_{2}} \right)=-1 \\
 & \Rightarrow 10\left( {{m}_{2}} \right)=-1 \\
 & \Rightarrow {{m}_{2}}=-\dfrac{1}{10} \\
\end{align}$
We know that general equation of a line is:
$y=mx+c$
Substituting the value of m as $-\dfrac{1}{10}$ in the above equation we get the equation of an altitude passing through$G\left( -3,4 \right)$ .
$y=\left( -\dfrac{1}{10} \right)x+c$…… eq. (2)
Now, satisfying the vertex H in the above equation by substituting x as -3 and y as 4 we get,
$\begin{align}
  & 4=\left( -\dfrac{1}{10} \right)\left( -3 \right)+c \\
 & \Rightarrow 4=\dfrac{3}{10}+c \\
\end{align}$
Subtracting $\dfrac{3}{10}$ on both the sides we get,
$\begin{align}
  & 4-\dfrac{3}{10}=c \\
 & \Rightarrow \dfrac{40-3}{10}=c \\
 & \Rightarrow \dfrac{37}{10}=c \\
\end{align}$
Substituting the above value of c in eq. (2) we get,
$\begin{align}
  & y=\left( -\dfrac{1}{10} \right)x+\dfrac{37}{10} \\
 & \Rightarrow 10y=-x+37 \\
 & \Rightarrow x+10y=37 \\
\end{align}$
From the above solution, we have found the equation of an altitude as $x+10y=37$.
Hence, the correct option is (d).

Note: Instead of solving the above question in the way we have solved above we can use the options to find the answer.
Like altitude is passing through the point $G\left( -3,4 \right)$ so we can check the correct option by substituting this point in all the options and see which equation is satisfying the point G.
Checking option (a) by substituting the point G in it we get,
The equation written in option (a) is:
$10x+y=-26$
Substituting the point $G\left( -3,4 \right)$ in the above equation we get,
$\begin{align}
  & 10\left( -3 \right)+4=-26 \\
 & \Rightarrow -30+4=-26 \\
 & \Rightarrow -26=-26 \\
\end{align}$
Hence, option (a) is satisfying the point G and now, to check the slope of this equation.
In the above solution, we have calculated the slope of the altitude so you can use that slope here to check the options. The slope of the altitude that we have calculated above is $-\dfrac{1}{10}$.
We know that the slope of the line $ax+by+c=0$ is equal to:
$m=-\dfrac{a}{b}$
$10x+y=-26$
The slope for the above line is:
$m=-\dfrac{10}{1}$
As you can see that the slope of the above line is not equal to the slope of the altitude so this option is not correct.
Similarly, we can check other options too.