Question

The taxi fare in a city is as follows: for the first kilometer, the fare is $Rs.8$ and for the subsequent distance, it is $Rs.5$ per km. Taking the distance covered as $x$ km and the total fare as $Rs.y$, write a linear equation for this information and draw its graph.

Answer 1

Hint: The given question is related to the formation of linear equations in two variables and the representation of a linear equation on a cartesian plane. Try to form a linear equation in two variables using the information given in the question.

Complete step-by-step answer:
We are given that the fare for the first kilometer is $Rs.8$. Let the total fare for the subsequent distance be $Rs.z$ . We are also given that the total fare for the journey is $Rs.y$ .
So, $y=8+z....(i)$
Now, to find the total fare for subsequent distance, we will use the information that the rate is $Rs.5$ per km.
Now, the total distance is given as $x$ km. So, after the first kilometer, the remaining distance will be $\left( x-1 \right)km$. So, the total fare for subsequent distance will be $Rs.5(x-1)$ . But we assumed it to be $Rs.z$.
So, the value of $z$ is given as $z=5(x-1)$ .
Substituting $z=5(x-1)$ in equation $(i)$ , we get
$y=8+5(x-1)$
$\Rightarrow y=5x+3....(ii)$ which is the required equation.
Now, to draw the graph, we will find any three points lying on the line and join them.
To find the first point, we will substitute $x=1$ in equation $(ii)$ .
On substituting $x=1$ in equation $(ii)$ , we get
$y=5+3=8$
So,$(1,8)$ is the first point.
For the second point, we will substitute $x=0$ in equation $(ii)$ .
 On substituting $x=0$ in equation $(ii)$ , we get
$y=0+3=3$
So,$(0,3)$ is the second point.
For the third point, we will substitute $x=2$ in equation $(ii)$ .
On substituting $x=2$ in equation $(ii)$ , we get,
$y=10+3=13$
So,$(2,13)$ is the first point.
So, the graph for the equation $y=5x+3$ is given as :

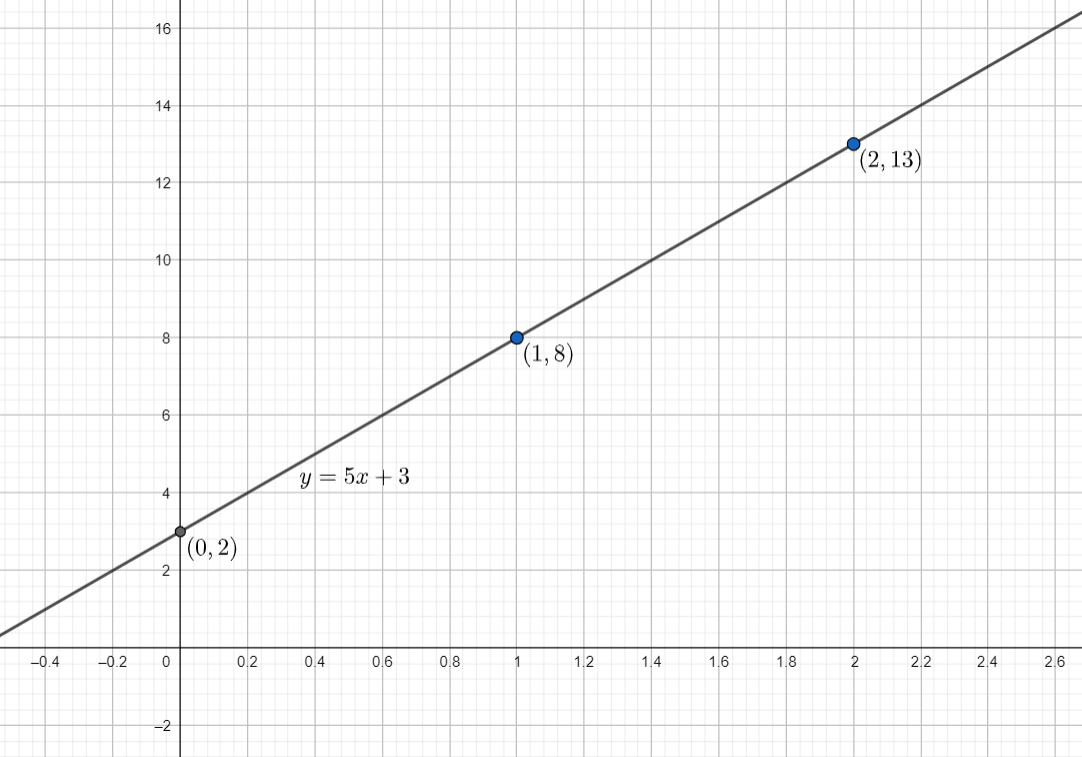
So, the equation for the given information is given as $y=5x+3$ and the graph is a straight line, passing through the points $(0,3)$ , $(1,8)$ and $(2,13)$ .

Note: While calculating the total fare for subsequent distance, many students make a mistake of taking distance as $x\,km$. For the subsequent journey, the distance will be $(x-1)\,km$ .