Question

The surface area of the cuboid is $758c{{m}^{2}}$. Its length and breadth are 14 cm and 11 cm respectively. Find its height.

Answer 1

Hint: We have given the surface area of cuboid along with that length and breadth are also given. We know that the formula for the surface area of the cuboid is $2\left( lb+bh+hl \right)$ where l, b and h are length, breadth and height of the cuboid respectively. Now, substitute the values of area, length and breadth given in the question in this formula of surface area of cuboid. After that solve this equation and we will get the value of “h” which is the height of the cuboid.

Complete step-by-step answer:
It is given that the surface area of cuboid is $758c{{m}^{2}}$ and length and breadth of the cuboid is equal to 14 cm and 11 cm respectively.
In the below diagram, we have drawn a cuboid having length, breadth and height as l, b and h respectively.

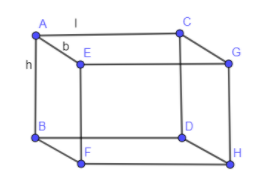
In the above diagram, we have shown length of AC by l, length of AE by b and length of AB by h.
We know that the formula of surface area of the cuboid is equal to:
$\text{Surface area}=2\left( lb+bh+hl \right)$……….. Eq. (1)
In the above formula, l, b and h are length, breadth and height of the cuboid respectively.
Substituting the value of l and b as 14 cm and 11 cm respectively and surface area as $758c{{m}^{2}}$ in eq. (1) we get,
$\begin{align}
  & 758=2\left( 14\left( 11 \right)+\left( 11 \right)h+h\left( 14 \right) \right) \\
 & \Rightarrow 758=2\left( 154+25h \right) \\
\end{align}$
Dividing 2 on both the sides of the above equation we get,
$\begin{align}
  & \dfrac{758}{2}=154+25h \\
 & \Rightarrow 379=154+25h \\
\end{align}$
Subtracting 154 on both the sides of the above equation we get,
$\begin{align}
  & 379-154=25h \\
 & 225=25h \\
\end{align}$
Dividing 5 on both the sides we get,
$\begin{align}
  & \dfrac{225}{25}=h \\
 & \Rightarrow 9cm=h \\
\end{align}$
Hence, the height of the cuboid is equal to 9 cm.

Note: In the above solution, you might get confused whether the surface area of the cuboid is the curved surface area or total surface area. The answer is you have to write total surface area in the formula of surface area so whenever surface area is given always write total surface area not curved surface area. Curved surface area is written when curved surface area or lateral surface area is given.