Question

The speed of a boat in still water is 15 km/hr. It goes 30 km upstream and returns downstream to its original point in 4 hour 30 minutes. Find the speed of the stream ( in km/hr).

Answer 1

Hint: Consider a boat moving in both upstream and downstream. During downstream, the boat moves in the same direction of stream and hence both the speeds are added. During upstream, the boat moves in the opposite direction of the stream and hence both the speeds are subtracted.

Formula used:
\[Time{\text{ }}taken{\text{ }}\left( t \right){\text{ }} = \dfrac{{{\text{Distance Travelled (d)}}}}{{Speed(v)}}\]

Complete step-by-step answer:
Given, Speed of a boat in still water is 15 km/hr , Distance Covered is 30 km, Total time taken during downstream and upstream is 4hr 30 min.
Let the speed of the stream be ‘x’ km/hr.
Speed of boat during downstream =(x+15) km/hr
Speed of boat during upstream =(15-x) km/hr
This question can be understood by the following figure drawn below:

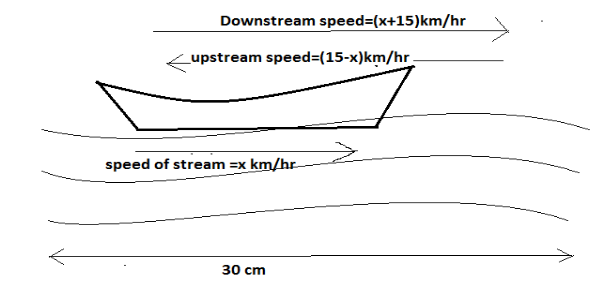
So, time taken by boat during downstream ($T_1$) =$\dfrac{{{\text{Distance Travelled}}}}{{Downstream{\text{ Speed}}}}$
$ \Rightarrow T_1 = \dfrac{{30}}{{x + 15}}hr$……………………… (i)
Now, time taken by boat during upstream ($T_2$) =$\dfrac{{{\text{Distance Travelled}}}}{{Upstream{\text{ Speed}}}}$
$ \Rightarrow T_2 = \dfrac{{30}}{{15 - x}}hr$………………………… (ii)
Total time taken during downstream and upstream (T) is 4hr 30 min.
$ \Rightarrow T = 4\dfrac{1}{2}hr$………………………………… (iii)
According to the question,
$
  {{T = T_1 + T_2}} \\
   \Rightarrow 4\dfrac{1}{2} = \dfrac{{30}}{{x + 15}} + \dfrac{{30}}{{15 - x}} \\
   \Rightarrow \dfrac{9}{2} = \dfrac{{30}}{{x + 15}} + \dfrac{{30}}{{15 - x}} \\
 $
Taking LCM on right hand side,we get :
$
   \Rightarrow \dfrac{9}{2} = \dfrac{{30\left( {x + 15 + 15 - x} \right)}}{{(x + 15)\left( {15 - x} \right)}} \\
   \Rightarrow \dfrac{9}{2} = \dfrac{{30 \times 30}}{{(x + 15)\left( {15 - x} \right)}} \\
   \Rightarrow \dfrac{9}{2} = \dfrac{{900}}{{(x + 15)\left( {15 - x} \right)}} \\
 $
Now, we cross –multiply both the sides, we get:
\[
   \Rightarrow 9\left( {x + 15} \right)\left( {15 - x} \right) = 2 \times 900 \\
   \Rightarrow 9\left( {x + 15} \right)\left( {15 - x} \right) = 1800 \\
   \Rightarrow \left( {15x - 15x + 225 - {x^2}} \right) = 200 \\
   \Rightarrow \left( { - {x^2} + 225} \right) = 200 \\
 \]
Simplifying the ‘x’, we get:
$ \Rightarrow {x^2} = 25$
Taking square root ,we get:
$
   \Rightarrow x = \sqrt {25} \\
   \Rightarrow x = \pm 5 \\
 $
But, we consider here only positive value of x, we have:
$\therefore x = 5{\text{ km/hr}}$

Thus, the speed of the stream is 5 km/hr.

Note: Time taken by boat during downstream is lesser than the time taken by boat during upstream. Whereas, the speed of boat during downstream is greater than the speed of boat during upstream.