Question

The sides of a pentagonal field (not regular) are $1737$ meters, $2160$ meters, $2358$ meters, $1422$ meters and $2214$ respectively. Find the greatest length of the tape by which the five sides may be measured completely.
A. $7$
B. $13$
C. $11$
D. $9$

Answer 1

Hint: Here we have been given a pentagon field (not regular) and we have to find the length of the tape by which we can measure the five sides completely. This means we have to find the HCF of all the five side length so that we can get a greatest common number whose length of tape can measure our pentagonal field. We will use prime factorization method for finding the HCF and get our desired answer.

Complete step by step answer:
The sides of a pentagonal field (not regular) are given as $1737$ meters, $2160$ meters, $2358$ meters, $1422$ meters and $2214$ respectively.So we can draw the pentagon as follows:

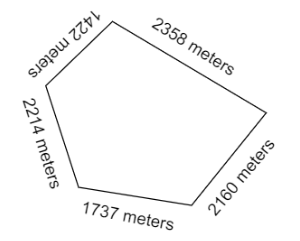
Now as we have to find the greatest length of the tape to measure the five sides we will find the HCF of all the five sides by using the Prime factorization method.Firstly we will find Prime factor of each sides as follows,

Prime factor of $1737$ can be calculated as,
$\begin{align}
  & \,\,\,\,\,3\left| \!{\underline {\,
  1737 \,}} \right. \\
 & \,\,\,\,\,3\left| \!{\underline {\,
  579 \,}} \right. \\
 & 193\left| \!{\underline {\,
  193 \,}} \right. \\
 & \,\,\,\,\,\,\,\,\left| \!{\underline {\,
  1 \,}} \right. \\
\end{align}$

Factors of $1737=3\times 3\times 197$ ….$\left( 1 \right)$
Prime factor of $2160$ can be calculated as,
$\begin{align}
  & 2\left| \!{\underline {\,
  2160 \,}} \right. \\
 & 2\left| \!{\underline {\,
  1080 \,}} \right. \\
 & 2\left| \!{\underline {\,
  540 \,}} \right. \\
 & 2\left| \!{\underline {\,
  270 \,}} \right. \\
 & 3\left| \!{\underline {\,
  135 \,}} \right. \\
 & 3\left| \!{\underline {\,
  45 \,}} \right. \\
 & 3\left| \!{\underline {\,
  15 \,}} \right. \\
 & 5\left| \!{\underline {\,
  5 \,}} \right. \\
 & \,\,\left| \!{\underline {\,
  1 \,}} \right. \\
\end{align}$

Factors of $2160=2\times 2\times 2\times 2\times 3\times 3\times 3\times 5$ ….$\left( 2 \right)$
Prime factor of $2358$ can be calculated as,
$\begin{align}
  & \,\,\,\,\,2\left| \!{\underline {\,
  2358 \,}} \right. \\
 & \,\,\,\,\,3\left| \!{\underline {\,
  1179 \,}} \right. \\
 & \,\,\,\,\,3\left| \!{\underline {\,
  393 \,}} \right. \\
 & 131\left| \!{\underline {\,
  131 \,}} \right. \\
 & \,\,\,\,\,\,\,\left| \!{\underline {\,
  1 \,}} \right. \\
\end{align}$

Factors of $2358=2\times 3\times 3\times 131$ ….$\left( 3 \right)$
Prime factor of $1422$ can be calculated as,
$\begin{align}
  & \,\,2\left| \!{\underline {\,
  1422 \,}} \right. \\
 & \,\,\,3\left| \!{\underline {\,
  711 \,}} \right. \\
 & \,\,\,3\left| \!{\underline {\,
  237 \,}} \right. \\
 & 79\left| \!{\underline {\,
  79 \,}} \right. \\
 & \,\,\,\,\,\left| \!{\underline {\,
  1 \,}} \right. \\
\end{align}$

Factors of $1422=2\times 3\times 3\times 79$ ….$\left( 4 \right)$
Prime factor of $2214$ can be calculated as,
$\begin{align}
  & 2\left| \!{\underline {\,
  2214 \,}} \right. \\
 & 3\left| \!{\underline {\,
  1107 \,}} \right. \\
 & \,\,3\left| \!{\underline {\,
  369 \,}} \right. \\
 & \,\,3\left| \!{\underline {\,
  123 \,}} \right. \\
 & 41\left| \!{\underline {\,
  41 \,}} \right. \\
 & \,\,\,\,\,\left| \!{\underline {\,
  1 \,}} \right. \\
\end{align}$
Factors of $2214=2\times 3\times 3\times 3\times 41$ ….$\left( 5 \right)$
So from equation (1), (2), (3), (4) and (5) we get the common factor as,
$\Rightarrow 3\times 3$
$\Rightarrow 9$
That means $9$ meter is the HCF of all five sides.So the greatest length of the tape by which the five sides can be measured completely is $9$ meters.

Hence the correct option is D.

Note: HCF is the highest common factor as we can see that all the five sides are of different length so for measuring the sides we need such a tape whose length is equal to the common factor of all the sides. We can get our answer by the first sides factor itself as our first side has the prime factor $3\times 3\times 197$ and $197$ is a prime number so the common factor can’t be greater than $3\times 3$ which is equal to $9$ also the common factor has to be a multiple of $3$ and in our option number smaller than $9$ is only $7$ which can’t be our answer. Hence our answer is $9$.