Question

The side of the square is 10 cm. Find the area of circumscribed and inscribed circles.

Answer 1

Hint- The side of the square is given in question. Inscribed circle means the circle which lies inside this given square and circumscribed is the circle present in outer of this square. So, use the concept that the diagonal of the square is the diameter of the circle circumscribed and the side acts as the diameter of the circle inscribed in the square.

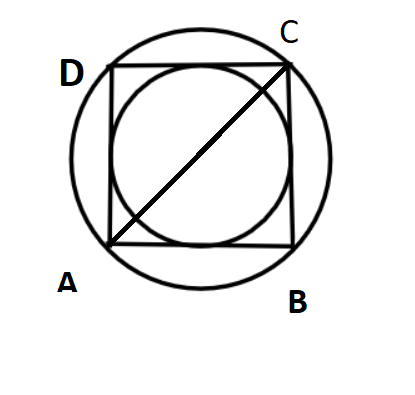
Now the side of a square AB=10cm.
So all sides are equal of a square hence AB=BC=CD=DA=10 cm
Thus all the sides will be equal to 10 cm only as the sides of the square are all equal.
So the diagonal of square is the diameter of the circumscribed circle thus
Diagonal AC will be using Pythagoras theorem in triangle ABC $hypotenou{s^2} = perpendicula{r^2} + bas{e^2}$
$ \Rightarrow A{C^2} = A{B^2} + B{C^2}$
Now AB=BC=10 cm (Sides of a square are equal)
$ \Rightarrow A{C^2} = {10^2} + {10^2} = 100 + 100 = 200$
Thus AC = $\sqrt {200} = 10\sqrt 2 {\text{ cm}}$……………………….. (1)
Now AC acts as diameter to the circumscribed circle hence
Diameter of circle circumscribed = $10\sqrt 2 {\text{ cm}}$
Thus $r = \dfrac{D}{2} = \dfrac{{10\sqrt 2 }}{2} = 5\sqrt 2 {\text{ cm}}$……………………. (2)
Now area of a given by Area = $\pi {r^2}$………………….. (3)
Putting equation (2) in equation (3)
Area = $\pi {(5\sqrt 2 )^2} = 3.14 \times 50 = 157{\text{ c}}{{\text{m}}^2}$
Now the side of the square will act as diameter to the circle inscribed to the square thus diameter of inscribed circle will be 10cm
Hence radius of inscribed circle = $\dfrac{{10}}{2} = 5{\text{ cm}}$……………………. (4)
Area of inscribed circle will be $\pi {(5)^2} = 3.14 \times 25 = 78.5{\text{ c}}{{\text{m}}^2}$ (Using equation 3 and 4)

Note- Whenever we face such problems the key concept we need to recall is the difference between the circumscribed and the inscribed circle of a square. By proper observation of the diagram it will be clear what will be the respective diameters of the circumscribed and the inscribed circle.