Question

The region represented by $\left| {x - y} \right| \leqslant 2$ and $\left| {x + y} \right| \leqslant 2$ is bounded by a:
$
  (a){\text{ Square of side length 2}}\sqrt 2 {\text{ units}}{\text{.}} \\
  (b){\text{ Rhombus of side length 2 units}}{\text{.}} \\
  (c){\text{ Square of area 16 sq units}}{\text{.}} \\
  (d){\text{ Rhombus of area 8}}\sqrt 2 {\text{ sq units}}{\text{.}} \\
    \\
 $

Answer 1

Hint – In this question we have been given two modulus functions, diagrammatic representation of the two given functions can help us in understanding the basic outline sketch of the problem that we are dealing with. Use the basic definitions of $\left| a \right| \leqslant x$ to understand the region which we are dealing with.

Complete step-by-step answer:

Given equation is
$\left| {x - y} \right| \leqslant 2$ and $\left| {x + y} \right| \leqslant 2$
Now according to property of modulus if$\left| a \right| \leqslant x$, then $a \leqslant x$ and $ - a \leqslant x$.
Then convert the equations according to this property we have,
$\left| {x - y} \right| \leqslant 2$
 $x - y \leqslant 2$………………… (1)
And $ - \left( {x - y} \right) \leqslant 2$
$ \Rightarrow - x + y \leqslant 2$………………….. (2)
Now, for equation $\left| {x + y} \right| \leqslant 2$
$x + y \leqslant 2$ …………………………. (3)
And $ - \left( {x + y} \right) \leqslant 2$
$ \Rightarrow - x - y \leqslant 2$ ……………………. (4)
Now plot all these equations
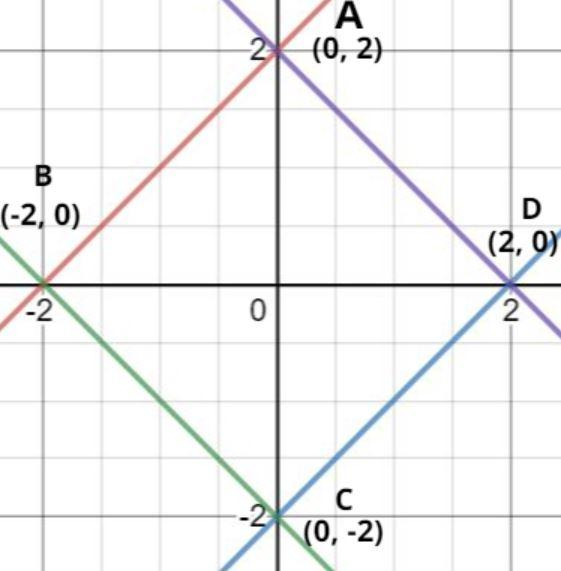
Equation (1) represents line CD (see figure) as x coefficient is positive and y coefficient is negative therefore line lie in fourth quadrant and the intersection point of this line with x and y axis are (2, 0) and (0, -2) (see figure).
Equation (2) represents line AB (see figure) as x coefficient is negative and y coefficient is positive therefore line lie in second quadrant and the intersection point of this line with x and y axis are (-2, 0) and (0, 2) (see figure).
Equation (3) represents line DA (see figure) as x coefficient is positive and y coefficient is positive therefore line lie in the first quadrant and the intersection point of this line with x and y axis are (2, 0) and (0, 2) (see figure).
Equation (4) represents line BC (see figure) as x coefficient is negative and y coefficient is negative therefore line lie in third quadrant and the intersection point of this line with x and y axis are (-2, 0) and (0, -2) (see figure).
Now all the lines are less than or equal to 2 so the region bounded by the curves is represented in the figure.
Now calculate the distance AB.
The distance between two points (a, b) and (c, d) is given as $d = \sqrt {{{\left( {c - a} \right)}^2} + {{\left( {d - b} \right)}^2}} $
Let the point A = (a, b) = (0, 2), point B = (c, d) = (-2, 0), point C = (e, f) = (0, -2), point D = (g, h) = (2, 0)
Now the distance $AB = \sqrt {{{\left( {c - a} \right)}^2} + {{\left( {d - b} \right)}^2}} = \sqrt {{{\left( { - 2 - 0} \right)}^2} + {{\left( {0 - 2} \right)}^2}} = \sqrt 8 = 2\sqrt 2 $
Now the distance $BC = \sqrt {{{\left( {e - c} \right)}^2} + {{\left( {f - d} \right)}^2}} = \sqrt {{{\left( {0 + 2} \right)}^2} + {{\left( { - 2 - 0} \right)}^2}} = \sqrt 8 = 2\sqrt 2 $
Now the distance $CD = \sqrt {{{\left( {g - e} \right)}^2} + {{\left( {h - f} \right)}^2}} = \sqrt {{{\left( {2 - 0} \right)}^2} + {{\left( {0 + 2} \right)}^2}} = \sqrt 8 = 2\sqrt 2 $
Now the distance $DA = \sqrt {{{\left( {g - a} \right)}^2} + {{\left( {h - b} \right)}^2}} = \sqrt {{{\left( {2 - 0} \right)}^2} + {{\left( {0 - 2} \right)}^2}} = \sqrt 8 = 2\sqrt 2 $
Now as we see all the distances are equal
$ \Rightarrow AB = BC = CD = DA$
So this is the condition of the square.
So, the region represented by given lines is a square with side length $2\sqrt 2 $ sq. unit.
Hence option (A) is correct.

Note – Whenever we face such types of problems the key concept is to have the basic understanding of modulus function, modulus function involving inequalities, definitions of rhombus, square and the basic area formula. This along with the curve outline sketch will help you reach the right answer.