Question

The ratio of in-radius and circum-radius of a square is
A. $1:\sqrt{2}$
B. $\sqrt{2}:\sqrt{3}$
C. $1:3$
D. $1:2$

Answer 1

Hint: To solve this question, we have to know the relation between the length of the side and the radii of circumcircle and incircle. Let us assume a square of side ‘a’ unit and let us construct an incircle in it. We can infer from figure-1 that the diameter of the incircle will be equal to the length of the side of the square. Similarly, from figure-2 we can infer that the diameter of the circumcircle will be equal to the length of the diagonal of the square. Using these relations, we can get the ratio of inradius to circumradius.

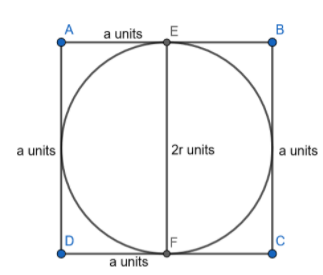
Figure -1

Figure -2

Complete step-by-step solution:
In the question, we are asked to find out the ratio of inradius to circumradius.
Let us consider a square of radius ‘a’ units. Let us construct an incircle in it. An incircle is defined as the circle which touches all the sides of a polygon. In our case, the polygon is a square.

Figure-3
The square ABCD is of side length ‘a’ unit. We can see that the circle in the diagram in the diagram is touching all the sides of the square. The lines AB and CD are tangents of the incircle.
The distance between the points on the circle whose tangents are parallel is equal to the diameter of the circle

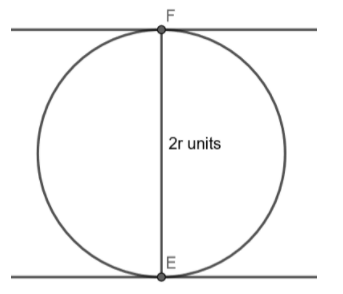
Figure -4
In the given circle of radius r units above, the points E, F have their tangents parallel to each other. The distance between E and F will be equal to the diameter. Similarly in the figure-3
As AB is parallel to CD, the distance between the sides AB and CD are equal to diameter= 2r units.
We also know that the distance between the sides of a square is equal to the length of the side itself. From this, we can write
$\begin{align}
  & a=2r \\
 & r=\dfrac{a}{2} \\
\end{align}$
Let us consider the same square of length ‘a’ units having a circumcircle around it. A circumcircle is a circle which passes through all the points of a polygon and in our case, square.

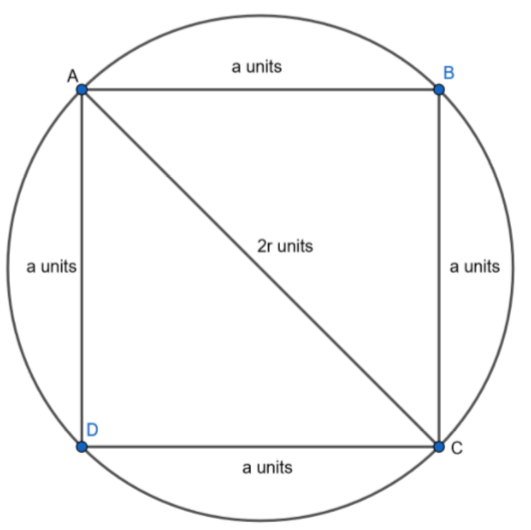
Figure-5
Circumcentre is the center of the circumcircle, from this we can infer that all the vertices of the square are equidistant from the circumcentre.

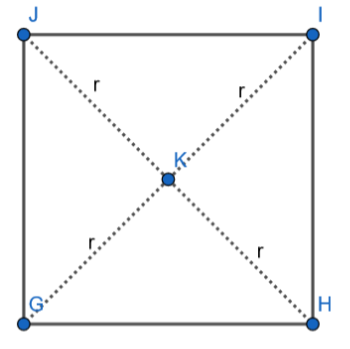
Let us consider a square GHIJ. We also know that the midpoint of the diagonal which is K is equidistant from all the vertices of the square. So, we can write that the length of the diagonal is equal to the diameter of the circumcircle.
From this property and figure-4 we can write
Diagonal length = $\sqrt{A{{D}^{2}}+D{{C}^{2}}}=\sqrt{{{a}^{2}}+{{a}^{2}}}=\sqrt{2{{a}^{2}}}=a\sqrt{2}$
As diagonal length = diameter of the circumcircle, we can write
$\begin{align}
  & a\sqrt{2}=2r \\
 & r=\dfrac{a\sqrt{2}}{2} \\
 & r=\dfrac{a}{\sqrt{2}} \\
\end{align}$
The ratio of inradius to circumradius can be written as
$ratio=\dfrac{\dfrac{a}{2}}{\dfrac{a}{\sqrt{2}}}=\dfrac{a}{2}\times \dfrac{\sqrt{2}}{a}=\dfrac{1}{\sqrt{2}}$
$\therefore $The required ratio is $1:\sqrt{2}$. Answer is option-A

Note: Students can be confused sometimes between incircle and circumcircle. Generally, in the polygons that we know, the incircle is a smaller circle that is inside a figure and the circumcircle is a larger circle that is outside the figure. Some students tend to draw the two circles in the same figure and end up doing calculation errors due to the complexity of the diagram. By drawing the two diagrams separately, we can get the answer clearly.