The radius and slant height of a cone are in the ratio 4:7. If its curved surface area is 792 ${\text{c}}{{\text{m}}^2}$, find its radius. ($\pi = \dfrac{{22}}{7}$)
Answer
Verified358.5k+ views
Hint: Here, we will proceed by assuming the radius and slant height of the cone as two different variables (r and l) and then we will use the formula for the curved surface area of the cone i.e., CSA = $\pi rl$.
Complete step-by-step answer:
Let the radius, the height and the slant height of a cone be r, h and l.
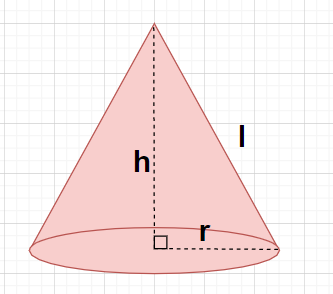
Given, ratio of the radius and the slant height of the cone is $\dfrac{r}{l} = \dfrac{4}{7}{\text{ }} \to {\text{(1)}}$
By cross multiplication of equation (1), we get
$
\Rightarrow 7r = 4l \\
\Rightarrow l = \dfrac{{7r}}{4}{\text{ }} \to {\text{(2)}} \\
$
Also given that the curved surface area of the cone is CSA = 792 ${\text{c}}{{\text{m}}^2}$
As we know that the curved surface of a cone of radius r and slant height l is given by CSA = $\pi rl{\text{ }} \to {\text{(3)}}$
$ \Rightarrow 792 = \pi rl$
By substituting the value of slant height l from equation (2) in the above equation, we get
$
\Rightarrow 792 = \pi r\left( {\dfrac{{7r}}{4}} \right) \\
\Rightarrow 792 = \left( {\dfrac{{22}}{7}} \right)r\left( {\dfrac{{7r}}{4}} \right) \\
\Rightarrow 792 = \dfrac{{11{r^2}}}{2} \\
\Rightarrow 11{r^2} = 792 \times 2 = 1584 \\
\Rightarrow {r^2} = \dfrac{{1584}}{{11}} = 144 \\
\Rightarrow r = \sqrt {144} = 12 \\
$
By putting r=12 in equation (2), the value of the slant height l will be given by
$ \Rightarrow l = \dfrac{{7r}}{4} = \dfrac{{7 \times 12}}{4} = 7 \times 3 = 21$
So, the slant height of the given cone is 21 cm.
Therefore, the radius of the given cone is 12 cm.
Note: In this particular problem, there are two unknowns (i.e., r and l) so in order to obtain the values of these unknowns we need two equations in terms of these two unknowns. Since, already one relation between the radius and the slant height is given in the problem statement and the other relation is obtained by using the formula for curved surface area of the cone.
Complete step-by-step answer:
Let the radius, the height and the slant height of a cone be r, h and l.
Given, ratio of the radius and the slant height of the cone is $\dfrac{r}{l} = \dfrac{4}{7}{\text{ }} \to {\text{(1)}}$
By cross multiplication of equation (1), we get
$
\Rightarrow 7r = 4l \\
\Rightarrow l = \dfrac{{7r}}{4}{\text{ }} \to {\text{(2)}} \\
$
Also given that the curved surface area of the cone is CSA = 792 ${\text{c}}{{\text{m}}^2}$
As we know that the curved surface of a cone of radius r and slant height l is given by CSA = $\pi rl{\text{ }} \to {\text{(3)}}$
$ \Rightarrow 792 = \pi rl$
By substituting the value of slant height l from equation (2) in the above equation, we get
$
\Rightarrow 792 = \pi r\left( {\dfrac{{7r}}{4}} \right) \\
\Rightarrow 792 = \left( {\dfrac{{22}}{7}} \right)r\left( {\dfrac{{7r}}{4}} \right) \\
\Rightarrow 792 = \dfrac{{11{r^2}}}{2} \\
\Rightarrow 11{r^2} = 792 \times 2 = 1584 \\
\Rightarrow {r^2} = \dfrac{{1584}}{{11}} = 144 \\
\Rightarrow r = \sqrt {144} = 12 \\
$
By putting r=12 in equation (2), the value of the slant height l will be given by
$ \Rightarrow l = \dfrac{{7r}}{4} = \dfrac{{7 \times 12}}{4} = 7 \times 3 = 21$
So, the slant height of the given cone is 21 cm.
Therefore, the radius of the given cone is 12 cm.
Note: In this particular problem, there are two unknowns (i.e., r and l) so in order to obtain the values of these unknowns we need two equations in terms of these two unknowns. Since, already one relation between the radius and the slant height is given in the problem statement and the other relation is obtained by using the formula for curved surface area of the cone.
Last updated date: 19th Sep 2023
•
Total views: 358.5k
•
Views today: 5.58k
