Question

What should be the pressure inside a small air bubble of 0.1mm radius situated just below the surface of water? Surface tension of water = \[72\times {{10}^{-3}}N{{m}^{-1}}\] and atmospheric pressure = \[1.013\times {{10}^{5}}N{{m}^{-2}}\].

Answer 1

Hint: The pressure difference inside the bubble in this case, when the air bubble is just below the surface of water is equal to \[\Delta p=\dfrac{2({{T}_{s}})}{r}\]. The final pressure inside the air bubble \[({{p}_{bubble}})\] is given by, \[{{p}_{bubble}}=\Delta p+{{p}_{out}}\], where \[{{p}_{out}}\] is the outer pressure, which in this case will be the atmospheric pressure.

Complete step by step answer:
Let’s start by understanding how to find the pressure inside the small air bubble when the air bubbles just below the surface of water. The excess pressure inside the air bubble, due to the air trapped inside the bubble is given by, \[{{p}_{bubble}}\]. However, there is also a pressure acting by the water just near the surface of the water, against the bubble. This outward pressure (\[{{p}_{out}}\]) is equal to the atmospheric pressure. Below is a diagram of the problem.

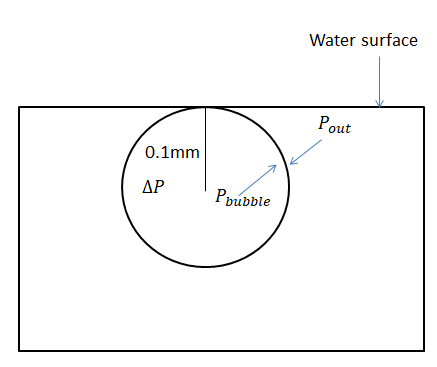
Hence, the net pressure difference inside the air bubble is given by, \[\Delta p={{p}_{bubble}}-{{p}_{out}}\].
Therefore, \[{{p}_{bubble}}=\Delta p+{{p}_{out}}=\dfrac{2({{T}_{s}})}{r}+1.013\times {{10}^{5}}N{{m}^{-2}}\Rightarrow {{p}_{bubble}}=2\dfrac{72\times {{10}^{-3}}N{{m}^{-1}}}{0.1\times {{10}^{-3}}m}+1.013\times {{10}^{5}}N{{m}^{-2}}\]
\[\Rightarrow {{p}_{bubble}}=0.0144\times {{10}^{5}}N{{m}^{-2}}+1.013\times {{10}^{5}}N{{m}^{-2}}\].
Therefore, the net pressure difference inside the air bubble is given by, \[{{p}_{bubble}}=1.027\times {{10}^{5}}N{{m}^{-2}}\].

Note:
It’s important to remember here that the air bubble is just below the surface of water. Hence, the net pressure difference in the water bubble is equal to the ratio of twice the surface tension of water is to the radius of the air bubble. That is, \[\Delta p=\dfrac{2({{T}_{s}})}{r}\]. Had the air bubble been above the surface of water, the net pressure difference inside the water bubble would have been equal to twice the pressure difference inside the bubble as in the previous case. That is, \[\Delta p=\dfrac{4({{T}_{s}})}{r}.\]

The reason behind the different values of pressures difference inside the bubble in different cases is because, when the air bubble is above the surface water, the outer surface of the bubble has its surface in contact with air, then the bubble made of water, then the bubble containing air and finally the water in contact with the surface of water. Hence, due to this the pressure difference inside the bubble in this case is, \[\Delta p=\dfrac{4({{T}_{s}})}{r}\].
When the bubble is just below the surface of water it has its outer surface in contact with water only, while in the previous case, the outer surface comes in contact with both air and water. Hence, the pressure inside the bubble in this case is, \[\Delta p=\dfrac{2({{T}_{s}})}{r}\].