
The points $C$ and $D$ on a semicircle with $AB$ as a diameter are such that $AC=1,$ $CD=2$ and $DB=3$. Then the length of $AB$lies in the interval.
A. $[4,4.1)$
B. $[4.1,4.2)$
C. $[4.2,4.3)$
D. $[4.3,\infty )$
Answer
604.5k+ views
Hint: To find the length of$AB$lies in which interval, first use Ptolemy’s theorem which is $AC.BD+AB.CD=BC.AD$. All values are given except $BC$ and $AD$, find it by using Pythagora's theorem. After that, substitute all values in Ptolemy’s equation and simplify it.
Complete step-by-step answer:
You will get the value of $x$. Consider a function $f(x)$for the equation of $x$and substitute $4,4.1,4.2,4.3$. You will get the root which lies between any of the options. Try it, you will get the answer.
In Mathematics, a semicircle is a one-dimensional locus of points that forms half of a circle. The full arc of a semicircle always measures $180{}^\circ $ (equivalently, $\pi $ radians, or a half-turn). It has only one line of symmetry (reflection symmetry). In non-technical usage, the term "semicircle" is sometimes used to refer to a half-disk, which is a two-dimensional geometric shape that also includes the diameter segment from one end of the arc to the other as well as all the interior points.
By Thales' theorem, any triangle inscribed in a semicircle with a vertex at each of the endpoints of the semicircle and the third vertex elsewhere on the semicircle is a right triangle, with right angle at the third vertex.
All lines intersecting the semicircle perpendicularly are concurrent at the center of the circle containing the given semicircle.
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for the diameter of a sphere.
In more modern usage, the length of a diameter is also called the diameter. In this sense one speaks of the diameter rather than a diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the radius $r$.
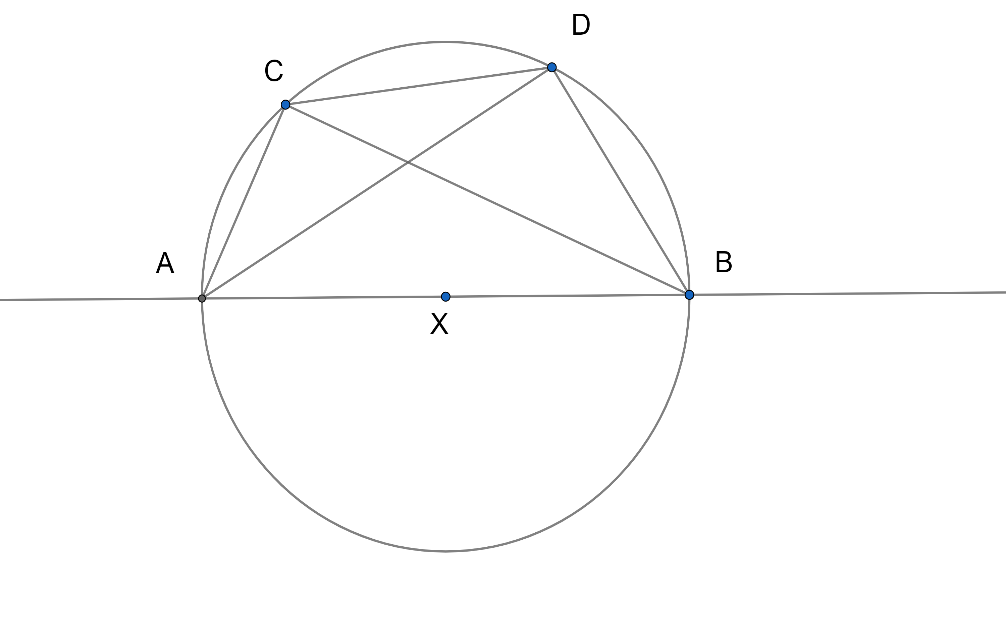
In the above figure, $ABCD$ is a cyclic quadrilateral.
$AB$ is the diameter of the circle.
Let, $AB=x$,
We have to use Ptolemy’s theorem,
Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral (a quadrilateral whose vertices lie on a common circle). The theorem is named after the greek astronomer and mathematician Ptolemy (Claudius Ptolemaeus). Ptolemy used the theorem as an aid to creating his table of chords, a trigonometric table that he applied to astronomy.
If the vertices of the cyclic quadrilateral are A, B, C, and D in order, then the theorem states that:
$AD.BC=AB.CD+BD.AC$
So using Ptolemy’s theorem, we get,
$AD.BC=AB.CD+BD.AC$
So here,
$AC=1,$ $CD=2$, $DB=3$, $AB=x$,
So in $\Delta ADB$, by Pythagoras theorem, we get,
$A{{B}^{2}}=A{{D}^{2}}+B{{D}^{2}}$
Substituting the values, we get,
\[\begin{align}
& {{x}^{2}}=A{{D}^{2}}+{{3}^{2}} \\
& {{x}^{2}}=A{{D}^{2}}+9 \\
& A{{D}^{2}}={{x}^{2}}-9 \\
\end{align}\]
\[AD=\sqrt{{{x}^{2}}-9}\] ………….. (1)
Now in $\Delta ACB$, by Pythagoras theorem, we get,
$A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}$
Substituting the values, we get,
$\begin{align}
& {{x}^{2}}={{1}^{2}}+B{{C}^{2}} \\
& {{x}^{2}}=1+B{{C}^{2}} \\
& B{{C}^{2}}={{x}^{2}}-1 \\
\end{align}$
$BC=\sqrt{{{x}^{2}}-1}$………………………. (2)
Now, $AD.BC=AB.CD+BD.AC$,
Substituting values in above we get,
$\sqrt{{{x}^{2}}-9}.\sqrt{{{x}^{2}}-1}=x.2+3.1$
Simplifying we get,
$3+2x=\sqrt{{{x}^{2}}-1}\times \sqrt{{{x}^{2}}-9}$
Squaring both sides we get,
${{\left( 3+2x \right)}^{2}}={{\left( \sqrt{{{x}^{2}}-1}\times \sqrt{{{x}^{2}}-9} \right)}^{2}}$
$\begin{align}
& 9+4{{x}^{2}}+12x=\left( ({{x}^{2}}-1)({{x}^{2}}-9) \right) \\
& 4{{x}^{2}}+12x+9={{x}^{4}}-10{{x}^{2}}+9 \\
& 4{{x}^{2}}+12x={{x}^{4}}-10{{x}^{2}} \\
& {{x}^{4}}-14{{x}^{2}}-12x=0 \\
& x({{x}^{3}}-14x-12)=0 \\
\end{align}$
So, $x\ne 0$ and $f(x)=({{x}^{3}}-14x-12)$
Here, $f(x)$ is a continuous function.
So now, first substituting $x=4$,
$f(4)=({{4}^{3}}-14(4)-12)=64-56-12=-4$
Now, $x=4.1$ we get,
$f(4.1)=({{(4.1)}^{3}}-14(4.1)-12)=68.921-57.4-12=-0.479$
Now substituting $x=4.2$ we get,
$f(4.2)=({{(4.2)}^{3}}-14(4.2)-12)=74.088-58.8-12=3.288$
For $x=4.3$ we get,
$f(4.3)=({{(4.3)}^{3}}-14(4.3)-12)=79.507-60.2-12=7.307$
Since, $f(x)$is a continuous function, therefore, one root of $f(x)$lies in $[4.1,4.2)$ .
So the length of $AB$lies in the interval $[4.1,4.2)$.
Note: Read the question carefully. Your concepts regarding the above question should be cleared. You should also know Ptolemy's theorem and Pythagoras theorem. While simplifying, do not miss any term. Also, take care that you do not make any silly mistakes.
Complete step-by-step answer:
You will get the value of $x$. Consider a function $f(x)$for the equation of $x$and substitute $4,4.1,4.2,4.3$. You will get the root which lies between any of the options. Try it, you will get the answer.
In Mathematics, a semicircle is a one-dimensional locus of points that forms half of a circle. The full arc of a semicircle always measures $180{}^\circ $ (equivalently, $\pi $ radians, or a half-turn). It has only one line of symmetry (reflection symmetry). In non-technical usage, the term "semicircle" is sometimes used to refer to a half-disk, which is a two-dimensional geometric shape that also includes the diameter segment from one end of the arc to the other as well as all the interior points.
By Thales' theorem, any triangle inscribed in a semicircle with a vertex at each of the endpoints of the semicircle and the third vertex elsewhere on the semicircle is a right triangle, with right angle at the third vertex.
All lines intersecting the semicircle perpendicularly are concurrent at the center of the circle containing the given semicircle.
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for the diameter of a sphere.
In more modern usage, the length of a diameter is also called the diameter. In this sense one speaks of the diameter rather than a diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the radius $r$.

In the above figure, $ABCD$ is a cyclic quadrilateral.
$AB$ is the diameter of the circle.
Let, $AB=x$,
We have to use Ptolemy’s theorem,
Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral (a quadrilateral whose vertices lie on a common circle). The theorem is named after the greek astronomer and mathematician Ptolemy (Claudius Ptolemaeus). Ptolemy used the theorem as an aid to creating his table of chords, a trigonometric table that he applied to astronomy.
If the vertices of the cyclic quadrilateral are A, B, C, and D in order, then the theorem states that:
$AD.BC=AB.CD+BD.AC$
So using Ptolemy’s theorem, we get,
$AD.BC=AB.CD+BD.AC$
So here,
$AC=1,$ $CD=2$, $DB=3$, $AB=x$,
So in $\Delta ADB$, by Pythagoras theorem, we get,
$A{{B}^{2}}=A{{D}^{2}}+B{{D}^{2}}$
Substituting the values, we get,
\[\begin{align}
& {{x}^{2}}=A{{D}^{2}}+{{3}^{2}} \\
& {{x}^{2}}=A{{D}^{2}}+9 \\
& A{{D}^{2}}={{x}^{2}}-9 \\
\end{align}\]
\[AD=\sqrt{{{x}^{2}}-9}\] ………….. (1)
Now in $\Delta ACB$, by Pythagoras theorem, we get,
$A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}$
Substituting the values, we get,
$\begin{align}
& {{x}^{2}}={{1}^{2}}+B{{C}^{2}} \\
& {{x}^{2}}=1+B{{C}^{2}} \\
& B{{C}^{2}}={{x}^{2}}-1 \\
\end{align}$
$BC=\sqrt{{{x}^{2}}-1}$………………………. (2)
Now, $AD.BC=AB.CD+BD.AC$,
Substituting values in above we get,
$\sqrt{{{x}^{2}}-9}.\sqrt{{{x}^{2}}-1}=x.2+3.1$
Simplifying we get,
$3+2x=\sqrt{{{x}^{2}}-1}\times \sqrt{{{x}^{2}}-9}$
Squaring both sides we get,
${{\left( 3+2x \right)}^{2}}={{\left( \sqrt{{{x}^{2}}-1}\times \sqrt{{{x}^{2}}-9} \right)}^{2}}$
$\begin{align}
& 9+4{{x}^{2}}+12x=\left( ({{x}^{2}}-1)({{x}^{2}}-9) \right) \\
& 4{{x}^{2}}+12x+9={{x}^{4}}-10{{x}^{2}}+9 \\
& 4{{x}^{2}}+12x={{x}^{4}}-10{{x}^{2}} \\
& {{x}^{4}}-14{{x}^{2}}-12x=0 \\
& x({{x}^{3}}-14x-12)=0 \\
\end{align}$
So, $x\ne 0$ and $f(x)=({{x}^{3}}-14x-12)$
Here, $f(x)$ is a continuous function.
So now, first substituting $x=4$,
$f(4)=({{4}^{3}}-14(4)-12)=64-56-12=-4$
Now, $x=4.1$ we get,
$f(4.1)=({{(4.1)}^{3}}-14(4.1)-12)=68.921-57.4-12=-0.479$
Now substituting $x=4.2$ we get,
$f(4.2)=({{(4.2)}^{3}}-14(4.2)-12)=74.088-58.8-12=3.288$
For $x=4.3$ we get,
$f(4.3)=({{(4.3)}^{3}}-14(4.3)-12)=79.507-60.2-12=7.307$
Since, $f(x)$is a continuous function, therefore, one root of $f(x)$lies in $[4.1,4.2)$ .
So the length of $AB$lies in the interval $[4.1,4.2)$.
Note: Read the question carefully. Your concepts regarding the above question should be cleared. You should also know Ptolemy's theorem and Pythagoras theorem. While simplifying, do not miss any term. Also, take care that you do not make any silly mistakes.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Who was the first woman to receive Bharat Ratna?

Write a letter to the principal requesting him to grant class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Discuss the main reasons for poverty in India




