Question

The points $A(a,0)$, $B(0,b)$, $C(c,0)$ and $D(0,d)$ are such that $ac=bd$ and $a$, $b$, $c$, $d$, are all non-zero. Then the points
A. form a parallelogram.
B. Do not lie on a circle.
C. form a trapezium.
D. are concyclic.

Answer 1

Hint: The points $A(a,0)$, $B(0,b)$, $C(c,0)$ and $D(0,d)$ are such that $ac=bd$ and $a$, $b$, $c$, $d$, are all non-zero and let $O$ be the origin. So here, $AO\times OC=OB\times OD$. From this you will get the answer.

Complete step-by-step answer:
A point is an exact position or location on a plane surface. It is important to understand that a point is not a thing, but a place. We indicate the position of a point by placing a dot with a pencil. This dot may have a diameter of, say, $0.2$mm, but a point has no size. No matter how far you zoomed in, it would still have no width. Since a point is a place, not a thing, it has no dimensions.
Points are usually named by using an upper-case single letter.
In another branch of mathematics called coordinate geometry, points are located on the plane using their coordinates - two numbers that show where the point is positioned with respect to two number line "axes" at right angles to each other.
In geometry, a set of points are said to be concyclic (or cocyclic) if they lie on a common circle. All concyclic points are the same distance from the center of the circle. Three points in the plane that do not all fall on a straight line are concyclic, but four or more such points in the plane are not necessarily concyclic.
Concyclic points are points that all lie on the same circle. This lesson will use some useful theorems to explain how to prove whether or not a set of two, three, or four points are concyclic.
A set of points is said to be concyclic if a circle passes through all of them. We have already seen that three non-collinear points are always concyclic, because there will always exist a (unique) circle passing through them. 

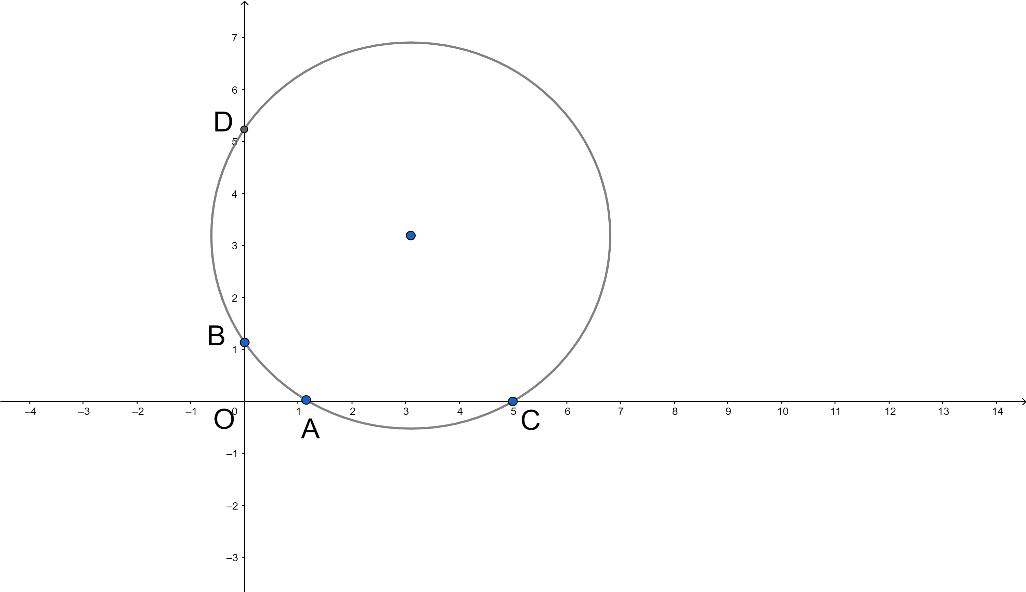
So we can see that,
The points $A(a,0)$, $B(0,b)$, $C(c,0)$ and $D(0,d)$ are such that $ac=bd$ and $a$, $b$, $c$, $d$, are all non-zero and $O$is the origin.
$AO\times OC=OB\times OD$
This is true in the case of a circle and two secants.
So points$A(a,0)$, $B(0,b)$, $C(c,0)$ and $D(0,d)$ lie on a circle.
So we can say that the given points are concyclic.
The correct answer is option(D).

Note: Read the question carefully. Also, you must know the concept behind the concyclic. Do not confuse yourself. Don’t jumble yourself.