Question

The perimeter of a right angled triangle is 30 cm and its hypotenuse is 13 cm. Find the length of the other two sides.

Answer 1

Hint: In this question first use the property that the perimeter of the triangle is the sum of all the sides, later on apply the concept of Pythagoras Theorem, so use these concepts to reach the solution of the question.

Complete step-by-step answer:

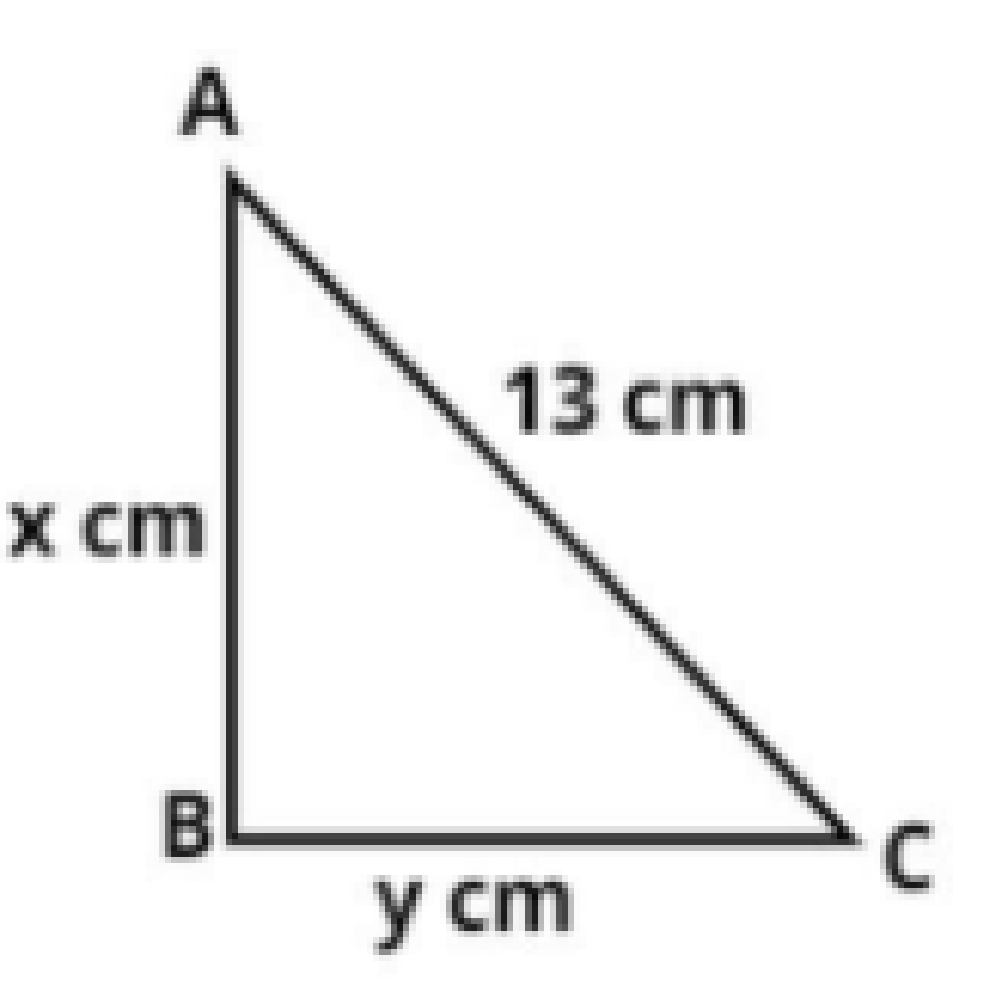
Let the right angled triangle be ABC as shown in figure which is right angled at B.
And it is given that the hypotenuse of the triangle is 13 cm.
$ \Rightarrow AC = 13{\text{ cm}}$.
Let the other two sides of the triangle be x and y respectively.
$ \Rightarrow AB = x{\text{ cm, }}BC = y{\text{ cm}}$.
Now, it is given that the perimeter of a right angled triangle is 30 cm.
So as we know that the perimeter of a triangle is the sum of all sides.
$
   \Rightarrow AB + BC + CA = 30 \\
   \Rightarrow x + y + 13 = 30 \\
   \Rightarrow x + y = 30 - 13 = 17 \\
   \Rightarrow x + y = 17{\text{ cm}}.............\left( 1 \right) \\
$
Now as triangle ABC is a right angled triangle so, apply Pythagoras Theorem, we have
${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}$
${\left( {AC} \right)^2} = {\left( {AB} \right)^2} + {\left( {BC} \right)^2}$
$
   \Rightarrow {13^2} = {x^2} + {y^2} \\
   \Rightarrow {x^2} + {y^2} = 169...........\left( 2 \right) \\
$
Now as we know that ${\left( {x + y} \right)^2} = {x^2} + {y^2} + 2xy$
Therefore from equation (1) and (2)
$
   \Rightarrow {17^2} = 169 + 2xy \\
   \Rightarrow 2xy = 289 - 169 \\
   \Rightarrow 2xy = 120 \\
   \Rightarrow xy = 60..........\left( 3 \right) \\
$
Now it is a known fact that ${\left( {x - y} \right)^2} = {\left( {x + y} \right)^2} - 4xy$
Therefore from equation (1) and (3).
$
   \Rightarrow {\left( {x - y} \right)^2} = {\left( {17} \right)^2} - 4 \times 60 \\
   \Rightarrow {\left( {x - y} \right)^2} = 289 - 240 = 49 \\
   \Rightarrow x - y = \sqrt {49} = 7.........\left( 4 \right) \\
$
Now add equation (1) and (4)
$
   \Rightarrow x + y + x - y = 17 + 7 \\
   \Rightarrow 2x = 24 \\
$
$ \Rightarrow x = 12$ cm.
Now from equation (1)
$
  x + y = 17 \\
   \Rightarrow 12 + y = 17 \\
   \Rightarrow y = 17 - 12 = 5 \\
$
$\therefore y = 5$ cm.
So, the length of the other two sides are 12 and 5 cm.
So, this is the required answer.

Note: Whenever we face such types of questions always remember that the perimeter of any figure is sum of all the sides, so use this property and construct the equation, later on apply the property of Pythagoras theorem and construct another equation then solve these two equations as above we will get the required length of the other sides of the triangle.