Question

The perimeter of a quadrant of a circle of radius $\dfrac{7}{2}cm$ is :
(a) $3.5cm$
(b) $5.5cm$
(c) $7.5cm$
(d) $12.5cm$

Answer 1

Hint:As we know that Circumference of circle is $2\pi r$ . Perimeter implies that the circumference of a circle and quadrant of a circle means one-fourth part of the circle. Using this concept we will get the required solution .

Complete step-by-step answer:
 As We learn that Perimeter of the circle is $2\pi r$.
But in this question we have to find the perimeter of a quadrant of circle means that one-fourth of the perimeter of circle
Here we see that the blue colored part is the quadrant of the circle .

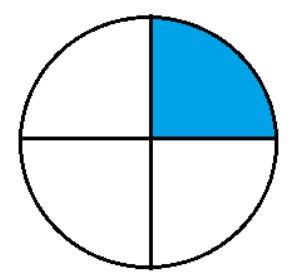
Perimeter of quadrant of circle is $\dfrac{{2\pi r}}{4}$
where we take $\pi = \dfrac{{22}}{7}$ and Radius of circle is given $r = \dfrac{7}{2}$ ;
By putting these value ,
= $\dfrac{{2 \times \dfrac{{22}}{7} \times \dfrac{7}{2}}}{4}$
When we solve we get
= $\dfrac{{22}}{4}$$cm$
In decimal form
= $5.5cm$

So, the correct answer is “Option B”.

Note:Students should also remembered that Area of Circle is = $\pi {r^2}$ And the area of quadrant is $\dfrac{{\pi {r^2}}}{4}$.Perimeter of semi-circle is $\pi r$ and Area of semi-circle is $\dfrac{{\pi {r^2}}}{2}$.
Perimeter of Square is $4 \times a$ and Area of Square is ${a^2}$ where a is the side of the square.
Perimeter of rectangle is $2\left( {l + b} \right)$ and Area of rectangle is $l \times b$ where $l = $ Length of Rectangle and $b = $ breadth of Rectangle.