Question

The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
A. 8a
B. 4a
C. 2a
D. 16a

Answer 1

Hint: We draw a circle having radius ‘a’ circumscribed inside a square. Use the property of sides of squares being equal to compare with the diameter of the circle. Use the formula of perimeter of square to find the perimeter.
* Perimeter of a square having side ‘x’ is 4x. A square is a quadrilateral having all four sides of equal length and having all angles as right angles.
* Circumscribed word means to enclose a figure within some bounds. When we say x circumscribing y we mean that y is enclosed completely within x.

Complete step-by-step solution:
We draw a figure where a square is circumscribing a circle of radius ‘a’.

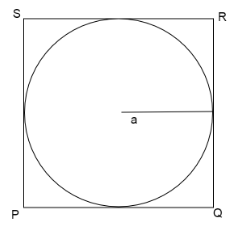
We know the perimeter of square PQRS is the sum of the lengths of all sides of the square.
\[ \Rightarrow \]Perimeter\[ = \left( {PQ + QR + RS + SP} \right)\]
Since all sides of the square are equal
So, \[PQ = QR = RS = SP\]
\[ \Rightarrow \]Perimeter\[ = \left( {PQ + PQ + PQ + PQ} \right)\]
\[ \Rightarrow \]Perimeter\[ = 4PQ\]....................… (1)
Now we know the radius of the circle is ‘a’.
Since diameter is twice the radius of the circle
\[ \Rightarrow \]Diameter of the circle\[ = 2a\]cm…………………..… (2)
If we draw diameter in such a way that it is parallel to the side of the square, then the length of the diameter is equal to the length of the side of the square.
\[ \Rightarrow PQ = 2a\]cm
Substitute the value of PQ in equation (1)
\[ \Rightarrow \]Perimeter of square PQRS \[ = \left( {4 \times 2a} \right)\]cm
\[ \Rightarrow \]Perimeter of square PQRS\[ = 8a\]cm
\[\therefore \]Perimeter of square is 8a (cm)

\[\therefore \]Correct option is A.

Note: Students are likely to make mistakes by drawing the opposite diagram, they tend to draw squares inside the circle. Keep in mind circumscribing means that the square has a circle inscribed in it.