Question

The particle executing simple harmonic motion has a kinetic energy of \[{{K}_{0}}{{\cos }^{2}}\omega t\]. The maximum values of the potential energy and the total energy are respectively
A. \[{{K}_{0}}\] and \[{{K}_{0}}\]
B. 0 and \[2{{K}_{0}}\]
C. \[\dfrac{{{K}_{0}}}{2}\] and \[{{K}_{0}}\]
D. \[{{K}_{0}}\] and \[2{{K}_{0}}\]

Answer 1

Hint: The given equation is in the form of simple harmonic motion. Simple harmonic motion is exhibited when a force is applied on an object and that object is moving with respect to the mean position. In simple harmonic motion, the applied force is directly proportional to the displacement of that object. Hence to maximum potential energy will be at the maximum displacement. According to the law of conservation of energy, we can find out the total energy from potential energy.

Complete Step-by-Step solution:
The energy diagram of a simple harmonic motion shown below.

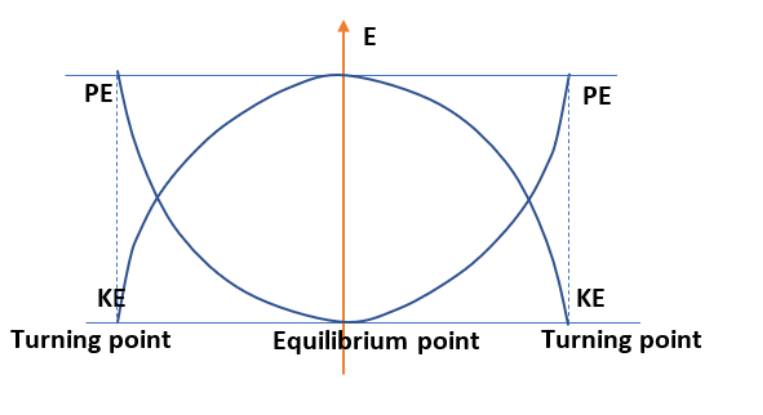
According to the simple harmonic motion at the extreme points, the kinetic energy will be zero and the potential energy will be the maximum.
\[\text{Total energy = Kinetic energy + Potential energy}\]
Therefore, at extreme points, the total energy will be the potential energy.
According to the given equation of simple harmonic motion, \[{{K}_{0}}\] represents the maximum energy. Because sinusoidal functions have a maximum value is 1.
Therefore, at extreme points, the maximum potential energy will be \[{{K}_{0}}\].
Since the maximum potential energy is \[{{K}_{0}}\], the total energy will also be \[{{K}_{0}}\].
Hence, the correct option is A.

Additional information:
Simple harmonic motion is a special kind of motion in which the acceleration of the object is always directly proportional to the distance from its centre of the path. This acceleration is always directed towards the centre.
Since the simple harmonic motion is analogous to the circular motion, the potential energy can be written as,
\[U=\dfrac{1}{2}m{{\omega }^{2}}{{x}^{2}}\], where m is the mass of the object, \[\omega \] is the angular frequency and x is the displacement.
At the maximum displacement, the potential energy will be the total energy.
\[E=\dfrac{1}{2}m{{\omega }^{2}}{{A}^{2}}\], where A is the amplitude (maximum displacement).
Kinetic energy can be written as,
\[K=\dfrac{1}{2}m{{v}^{2}}\], where m is the mass of the object and v is the velocity of the object.
Hence the total energy can be written as,
\[E=K+U\]
\[\dfrac{1}{2}m{{\omega }^{2}}{{A}^{2}}=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}m{{\omega }^{2}}{{x}^{2}}\]
\[{{\omega }^{2}}{{A}^{2}}={{v}^{2}}+{{\omega }^{2}}{{x}^{2}}\]
\[{{v}^{2}}={{\omega }^{2}}{{A}^{2}}-{{\omega }^{2}}{{x}^{2}}\]
\[{{v}^{2}}={{\omega }^{2}}({{A}^{2}}-{{x}^{2}})\]
\[v=\pm \sqrt{{{\omega }^{2}}({{A}^{2}}-{{x}^{2}})}\]
\[v=\omega \sqrt{({{A}^{2}}-{{x}^{2}})}\]
Angular frequency can be written as,
\[\omega =2\pi f\]
\[v=\pm 2\pi f\sqrt{({{A}^{2}}-{{x}^{2}})}\]
This equation can be used to find the velocity of the object at any position in its simple harmonic motion.

Note: Since the motion is a simple harmonic motion, the applied force is directly proportional to the displacement of the body from the mean position. So, the maximum displacement will be at the extreme points. Here we are taking maximum displacement to find the total energy. At turning points or extreme points, the potential energy will be maximum.