Question

The number of students in a hostel speaking different languages is given below :

Language	Tamil	Telugu	Malayalam	Kannada	English	Others
Number of students	36	12	9	6	5	4

Represent the data in a pie chart.

Answer 1

Hint: To draw a pie chart we need to find a central angle for each language. And the central angle is given by $\dfrac{{{\text{number of students speaking that language}}}}{{{\text{total number of students}}}}\times 360$. Using this we need to find the central angle for each language and then draw a circle of any radius and placing the protractor on the horizontal radius we need to mark the central angle and repeat the process for all the languages.

Complete step by step solution:
Here we are given the number of students speaking each language
To draw a pie chart we need to find a central angle for each language
And the central angle is given by $\dfrac{{{\text{number of students speaking that language}}}}{{{\text{total number of students}}}}\times 360$
So the total number of students is given by
$ \Rightarrow 36 + 12 + 9 + 6 + 5 + 4 = 72$
So let's find the central angle for each language
The number of students speaking tamil is 36
$
   \Rightarrow \dfrac{{36}}{{72}}\times 360 \\
   \Rightarrow \dfrac{1}{2}\times 360 \\
   \Rightarrow \dfrac{{360}}{2} = 180 \\
 $
Hence the central angle for tamil is ${180^ \circ }$
The number of students speaking telugu is 12
$
   \Rightarrow \dfrac{{12}}{{72}}\times 360 \\
   \Rightarrow \dfrac{1}{6}\times 360 \\
   \Rightarrow \dfrac{{360}}{6} = 60 \\
 $
Hence the central angle for telugu is ${60^ \circ }$
The number of students speaking malayalam is 9
$
   \Rightarrow \dfrac{9}{{72}}\times 360 \\
   \Rightarrow \dfrac{1}{8}\times 360 \\
   \Rightarrow \dfrac{{360}}{8} = 45 \\
 $
Hence the central angle for malayalam is ${45^ \circ }$
The number of students speaking kannada is 6
$
   \Rightarrow \dfrac{6}{{72}}\times 360 \\
   \Rightarrow \dfrac{1}{{12}}\times 360 \\
   \Rightarrow \dfrac{{360}}{{12}} = 30 \\
 $
Hence the central angle for kannada is ${30^ \circ }$
The number of students speaking english is 5
$
   \Rightarrow \dfrac{5}{1}\times 5 \\
   \Rightarrow 5\times 5 = 25 \\
 $
Hence the central angle for english is ${25^ \circ }$
The number of students speaking other language are 4
$
   \Rightarrow \dfrac{4}{{72}}\times 360 \\
   \Rightarrow \dfrac{1}{{18}}\times 360 \\
   \Rightarrow \dfrac{{360}}{{18}} = 20 \\
 $
Hence the central angle for other language is ${20^ \circ }$
To draw a pie chart we need to draw a circle with any radius.

Draw the horizontal radius

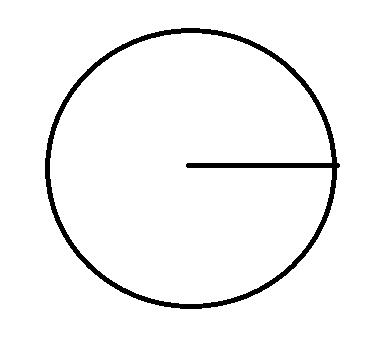
Now place the protractor on the radius and mark the angle for tamil.

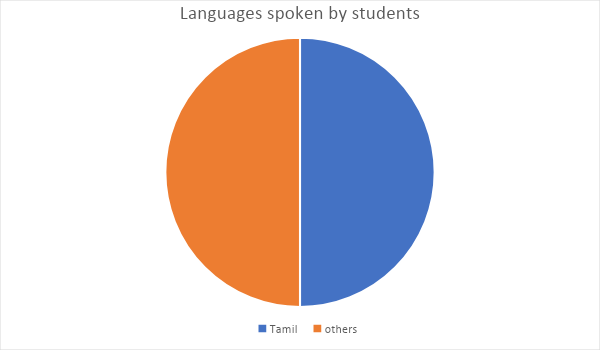
now place the protractor on the line drawn for tamil and mark the angle for telugu.

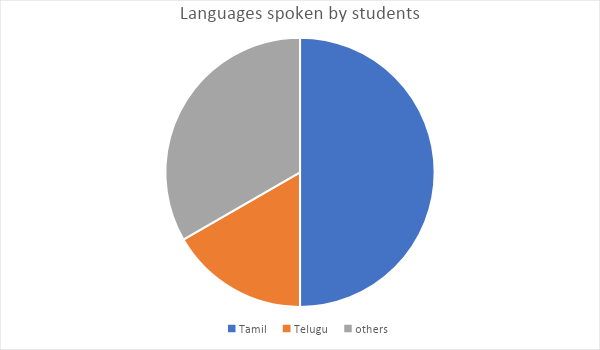
And we need to repeat this procedure for all the languages.

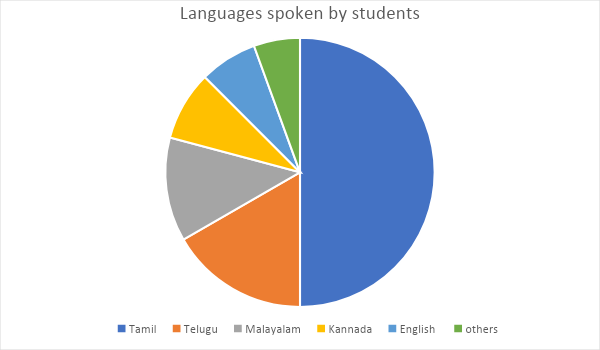
Hence the pie chart is obtained.

Note :
Pie charts are generally used to show percentage or proportional data and usually the percentage represented by each category is provided next to the corresponding slice of pie. Pie charts are good for displaying data for around 6 categories or fewer.
If the data is given in percentage then the central angle is given by $\dfrac{{{\text{percentage value of the component}}}}{{100}}\times 360$.