Question

The number of soaps of size $10{\text{ cm}} \times 5{\text{ cm}} \times 2.5{\text{ cm}}$ that can be put in the box of a cuboid of size of $20{\text{ cm}} \times 10{\text{ cm}} \times 10{\text{ cm}}$.

Answer 1

Hint: First find the volume of the soap using the given dimension of soap and then find the volume of the cuboid box using the given dimension of box and then divide the volume of box with the volume of soap to get the desired result.

Formula used:
Volume of cuboid \[ = {\rm{length}} \times {\rm{width}} \times {\rm{height}}\], Number of soaps \[ = \dfrac{{{\rm{Volume\, of\, box}}}}{{{\rm{Volume\, of\, soap}}}}\]

Complete step-by-step answer:
It is given to us that the size of the soap is $10{\text{ cm}} \times 5{\text{ cm}} \times 2.5{\text{ cm}}$ and the size of the cuboid box is $20{\text{ cm}} \times 10{\text{ cm}} \times 10{\text{ cm}}$.

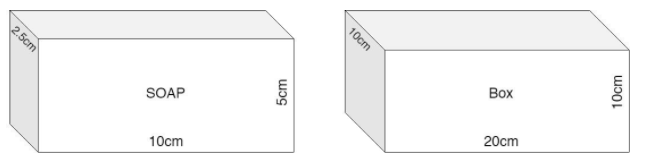
We have to find the number of soaps that can be put in the cuboid box.
First find the volume of the soap using the given dimension of soap.
We know that the soap has the shape of a cuboid whose length is given as $10$ cm, width is $5$ cm and height is given as $2.5$ cm.
We also know that the volume of cuboid is given as the product of length, width and height.
Volume of soap$ = {\text{length}} \times {\text{width}} \times {\text{height}}$
Substitute length as $10$ cm, width as $5$ cm and height as $2.5$ cm in the above formula.
Volume of soap $ = 10 \times 5 \times 2.5$
Volume of soap $ = 125$
So, we get that the volume of the soap is $125{\text{ c}}{{\text{m}}^3}$.
Now, we find the volume of the cuboid box. It is already given that the shape of the box is cuboid and the length, width and height of the box are given as $20{\text{ cm,10 cm, and 10 cm}}$ respectively.
Volume of cuboid box $ = {\text{length}} \times {\text{width}} \times {\text{height}}$
Substitute length as 20 cm, width as 10 cm and height as 10 cm in the formula.
Volume of cuboid box $ = 20 \times 10 \times 10$
Volume of cuboid box $ = 2000$
So, we get that the volume of the cuboid box is $2000{\text{ c}}{{\text{m}}^3}$.
We can find the number of soaps by dividing the volume of the box with the volume of a soap.
Number of soaps $ = \dfrac{{{\text{Volume of box}}}}{{{\text{Volume of soap}}}}$
Substitute the volume of box as $2000{\text{ c}}{{\text{m}}^3}$ and the volume of soap $125{\text{ c}}{{\text{m}}^3}$into the above formula:
Number of soaps $ = \dfrac{{2000}}{{125}}$
Number of soaps $ = 16$
So, we can put 16 soaps in the given box.
Hence, the option (B) is correct.

Note: To solve these types of questions, we must remember the formulas of the volumes. Hence, in this question the number of soaps can be found by dividing the volume of the box with the volume of a soap. Similarly, we can solve these types of questions using the above method.