
The number of rotational symmetry which a semicircle has
A) $0$
B) $1$
C) $2$
D) Infinite
Answer
579.6k+ views
Hint: A figure has rotational symmetry if it coincides with itself in a rotation less than ${360^ \circ }$. The order of rotation of a figure is the number of times it coincides with itself in a rotation less than ${360^ \circ }$. The angle of rotation for a regular figure is ${360^ \circ }$ divided by the order of rotation.
Complete step-by-step answer:
In the present question,
We are asked to find out the number of rotational symmetries that a semi-circle has. Before answering that we must know about what is rotational symmetry.
A figure has rotational symmetry if it coincides with itself in a rotation less than ${360^ \circ }$. The order of rotation of a figure is the number of times it coincides with itself in a rotation less than ${360^ \circ }$. The angle of rotation for a regular figure is ${360^ \circ }$ divided by the order of rotation.
For example, if we take a rectangle and rotate it by ${180^ \circ }$ then also we will get the same figure which coincides with the previous rectangle.
Hence, we can say that a rectangle has one rotational symmetry. Now, if we talk about the order of the rotational symmetry, it is simply the number of rotational symmetries possible.
If we take a circle as a n example, for every small rotation also it will look the same. So, a circle has an infinite number of rotational symmetries.
But we are asked to find out for the semi-circle. Let us check whether there is any possibility of rotational symmetry for a semi-circle.
Let us draw diagrams to check that,
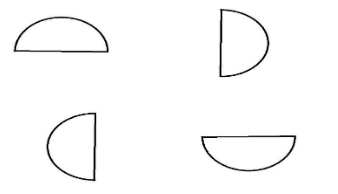
From the above diagrams, we can conclude that the semi-circle does not have any rotational symmetry.
Because, it does not coincide with itself in any rotation less than ${360^ \circ }$.
Hence the option A is the correct answer.
Note: In the present question, we are asked to find out the rotational symmetry of a semicircle. It would be better if we draw on the paper and make some trials rather than only imagining. We need to check every possible step and should not miss any step while listing different possibilities. When we are asked to find out different random shapes, we must check by drawing it on paper. This could help us in getting the accurate answer.
Complete step-by-step answer:
In the present question,
We are asked to find out the number of rotational symmetries that a semi-circle has. Before answering that we must know about what is rotational symmetry.
A figure has rotational symmetry if it coincides with itself in a rotation less than ${360^ \circ }$. The order of rotation of a figure is the number of times it coincides with itself in a rotation less than ${360^ \circ }$. The angle of rotation for a regular figure is ${360^ \circ }$ divided by the order of rotation.
For example, if we take a rectangle and rotate it by ${180^ \circ }$ then also we will get the same figure which coincides with the previous rectangle.
Hence, we can say that a rectangle has one rotational symmetry. Now, if we talk about the order of the rotational symmetry, it is simply the number of rotational symmetries possible.
If we take a circle as a n example, for every small rotation also it will look the same. So, a circle has an infinite number of rotational symmetries.
But we are asked to find out for the semi-circle. Let us check whether there is any possibility of rotational symmetry for a semi-circle.
Let us draw diagrams to check that,
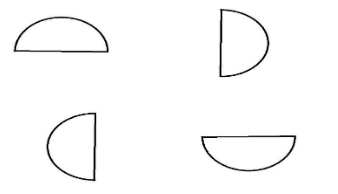
From the above diagrams, we can conclude that the semi-circle does not have any rotational symmetry.
Because, it does not coincide with itself in any rotation less than ${360^ \circ }$.
Hence the option A is the correct answer.
Note: In the present question, we are asked to find out the rotational symmetry of a semicircle. It would be better if we draw on the paper and make some trials rather than only imagining. We need to check every possible step and should not miss any step while listing different possibilities. When we are asked to find out different random shapes, we must check by drawing it on paper. This could help us in getting the accurate answer.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is the Full Form of ISI and RAW

Golden Revolution is related to AFood production BOil class 9 social science CBSE




