Question

The number of real roots of the equation ${e^{x - 1}} + x - 2 = 0$is
A.1
B.2
C.3
D.4

Answer 1

Hint: We are required to find the number of roots of the given equation. For that, we will re – arrange the equation and we will use a graphical method to solve this question. First, we will plot the graph of ${e^{x - 1}}$and then we will plot the graph of y = 2 – x. we will check the number of points of intersection between both the graphs and the total number of points of intersection will be the number of real roots of the equation.

Complete step-by-step answer:
We need to find the number of real roots of the equation ${e^{x - 1}} + x - 2 = 0$.
Let us re – arrange the given equation as:
${e^{x - 1}} + x - 2 = 0$ $ \Rightarrow {e^{x - 1}} = 2 - x$
Now considering ${e^{x - 1}}$ as a function g (x) and 2 – x as another function h (x).
Upon plotting the graphs of both the functions g (x) and h (x), we get

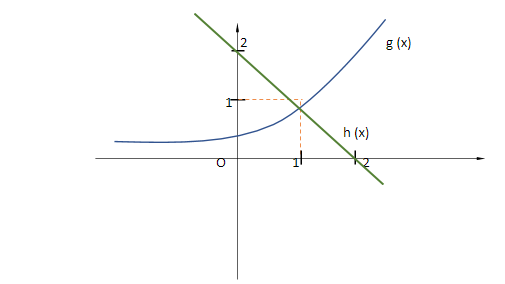
Here, we get only one intersection point between the graph of the curves g (x) = ${e^{x - 1}}$and h (x) = 2 – x.
Hence, we can say that the number of real roots of the given equation ${e^{x - 1}} + x - 2 = 0$ is only one.
Therefore, option(A) is correct.

Note:In such kind of problems, we can choose any procedure (method) to solve the given equation for its roots i. e., either graphical method or analytical method to solve with. We can also solve this question with the help of analytical methods. Take care while plotting the graphs because here as well we need to plot the graph of ${e^{x - 1}}$ but not of ${e^x}$.