Question

What should be the minimum height of a plane mirror so that a 6ft tall man can see his full view image standing in front of the mirror?
A. 6ft
B. 12ft
C. 3ft
D. 2ft

Answer 1

Hint: To solve this question you should know the laws of reflection. In addition, you must have the knowledge of geometry and the rules for congruence of triangles. Draw a diagram of a man standing in front of a mirror for better understanding.

Complete answer:
We know that the image formed in a plane mirror is real and erect. The size of the image is the same as the size of the object.
Consider a man of height H standing in front of a large mirror. An image of the same height will be formed at the same point as the object from the mirror, in the mirror.
Now, the man will see his full image when all the light rays from his whole body will enter his eyes after reflection. For this, the light ray coming from the tip of his head should reflect on the mirror and enter his eyes. Even the light ray coming from his bottom of his feet should reflect and enter his eyes. To understand this better look at the given figure.

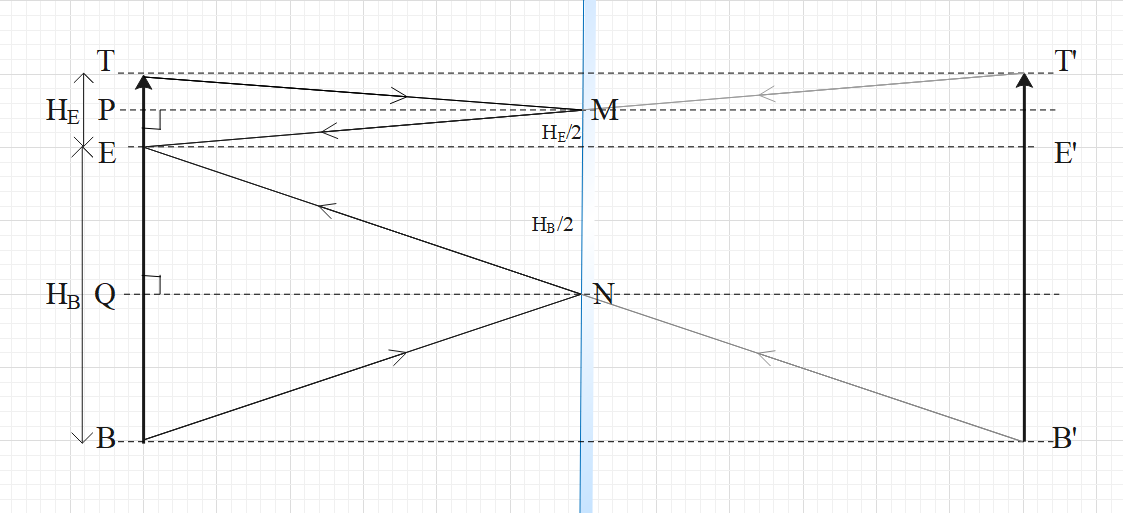
${{H}_{E}}$ is the distance of the tip of his head to his eyes.
${{H}_{B}}$ is the distance of the bottom of his feet to his eyes.
PM and QN are normal drawn at the point of reflection.
According to the laws of reflection, the angle of incidence and angle of reflection are equal .……..(statement 1).
Consider $\Delta TPM$ and $\Delta EPM$.
Here, $\angle PMT=\angle PEM$ (according to statement 1).
$\angle TPM=\angle EPM$ (Since both are equal to 90 degrees).
PM is the common side for both the triangles. Therefore, $\Delta TPM\cong \Delta EPM$ by ASA rule of congruence.
If $\Delta TPM\cong \Delta EPM$ then TP = EP.
Similarly, $\Delta EQN\cong \Delta BQN$ and EQ = BQ.
Since, $TP+EP={{H}_{E}}$ and TP = EP, $2EP={{H}_{E}}$.
$\Rightarrow EP=\dfrac{{{H}_{E}}}{2}$.
Similarly, $2EQ={{H}_{B}}$
$\Rightarrow EQ=\dfrac{{{H}_{B}}}{2}$.
According to the figure, $\dfrac{{{H}_{E}}}{2}+\dfrac{{{H}_{B}}}{2}={{H}_{M}}$ …….(i).
But, ${{H}_{E}}+{{H}_{B}}=H$ …….(ii).
From equations (i) and (ii) we get,
$\dfrac{{{H}_{E}}+{{H}_{B}}}{2}={{H}_{M}}\Rightarrow \dfrac{H}{2}={{H}_{M}}$.
Therefore, the height of the mirror that is required to see our full image is equal to half of our height.
It is given that H=6ft.
${{H}_{M}}=\dfrac{H}{2}=\dfrac{6}{2}=3ft$

So, the correct answer is “Option C”.

Note:
To see our full image in a plane mirror, a mirror half of our height is the only requirement. The distance of us from the mirror does not matter because we never used that distance in the solution. However, the mirror of the required size must be placed vertical at a height of $\dfrac{{{H}_{B}}}{2}$ from the ground, as shown in the figure.