Question

The minimum coefficient of friction ${{\mu }_{\min }}$ between a thin homogeneous rod and a floor at which a person can slowly lift the rod from the floor without slippage to the vertical position, applying to it a force perpendicular to it is $\dfrac{1}{x\sqrt{x}}$. Find the value of $x$.

Answer 1

Hint: We can find the value of coefficient of friction by finding the ratio of the resistive force and the value of normal or perpendicular force. The force of friction always acts in the direction opposite to the direction of intended or actual motion.

Formula used:
$T=Fr\sin \theta $
Where $T$is the torque, $F$ is the force, $r$ is the radius and $\theta $ is the angle between $F$ and lever arm

Complete step by step answer:
Coefficient of friction is described as the ratio of the force of friction between two bodies and the force pressing them together. It is a value that represents the relationship between two objects and the normal force or reaction between the objects. Coefficient of friction is of two types, Static and Kinetic coefficient of friction. Static coefficient of friction is applied to the stationary bodies while Kinetic coefficient is applied to the bodies in motion. Stationary or motionless objects experience more friction than those which are already in motion. We can say that it requires more force to put an object in motion than to sustain them in motion.
In the above question we are given that the rod does not slip on the floor, meaning we can apply the equations to equate all the forces as the rod is in equilibrium.
The forces acting on the rod are – gravitational force, applied force and the torque about the point of intersection of gravitational and applied force.

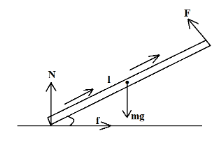
$\begin{align}
  & \text{Gravitational force = }mg \\
 & \text{Applied force = }F \\
 & \text{Torque = }T \\
 & \text{Angle of torque = }\alpha \\
\end{align}$

Balancing all the forces and torque acting on the rod,

$\sum\limits_{{}}^{{}}{T=Nl\cos \alpha -fl\left( \dfrac{1}{\sin \alpha }+\sin \alpha \right)}=0$
Where $N$i s the normal force and $f$ is the force of friction

The moment arm for normal force $N$ is $l\cos \alpha $ while for friction it is $l\left( \dfrac{1}{\sin \alpha }+\sin \alpha \right)$
From above equation we get,

\[\begin{align}
  & f=N\left( \dfrac{\cos \alpha \times \sin \alpha }{1+{{\sin }^{2}}\alpha } \right)=N\left( \dfrac{\cos \alpha \times \sin \alpha }{2{{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha } \right) \\
 & f=N\left( \dfrac{\cos \alpha \times \sin \alpha }{2\tan \alpha +\cot \alpha } \right) \\
\end{align}\]

Also, the force of friction cannot exceed $\mu N$, we have

$\mu \ge \dfrac{1}{2\tan \alpha +\cot \alpha }$

For minimum value of$\mu $, $2\tan \alpha +\cot \alpha $should be maximum

 $\begin{align}
  & \dfrac{d(2\tan \alpha +\cot \alpha )}{dx}=0 \\
 & 2{{\sec }^{2}}\alpha -\cos e{{c}^{2}}\alpha =0 \\
 & \tan \alpha =\dfrac{1}{\sqrt{2}} \\
\end{align}$
We get$\mu =\dfrac{1}{2\sqrt{2}}$
Comparing with$\dfrac{1}{x\sqrt{x}}$,
Value of $x=2$

Note:
While calculating the torque, always choose a point where maximum lines of forces are passing so that the number of resultant torques will be minimum. For no confusion, choose clockwise direction as positive and anti-clockwise as negative.