Question

The mid points of the sides of a triangle are $\left( {5,0} \right)$,$\left( {5,12} \right)$ and $\left( {0,12} \right)$, then orthocentre of this triangle is?
A.$\left( {0,0} \right)$
B.$\left( {0,24} \right)$
C.$\left( {10,0} \right)$
D.None of these

Answer 1

Hint: We can find the vertices of the triangle using mid-point formula. Then we can check whether the triangle is right-angled. We can find the coordinates of the orthocenter.

Complete step by step answer:

Given the mid points of the sides of a triangle are $\left( {5,0} \right)$,$\left( {5,12} \right)$ and $\left( {0,12} \right)$.
We can plot the given points as midpoints of a triangle.

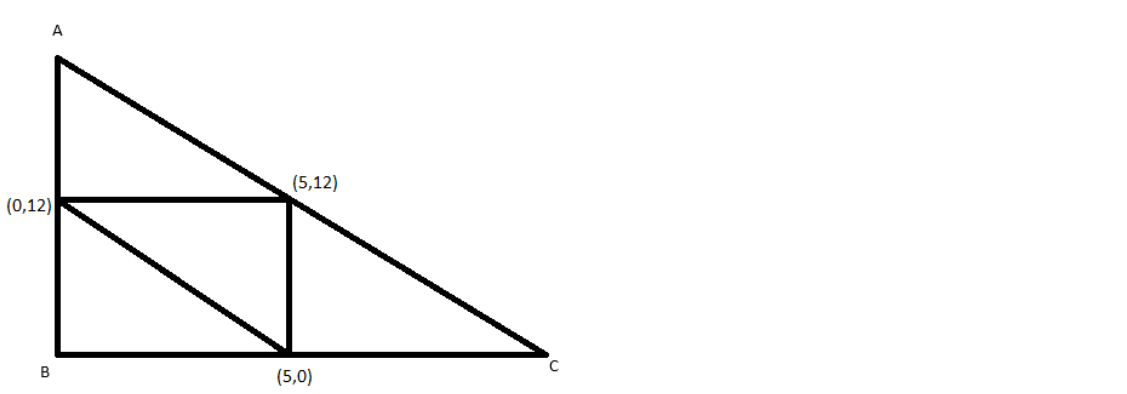
Let A$({x_1},{y_1})$, B$({x_2},{y_2})$and C$({x_3},{y_3})$ be the vertices of the triangle. We can use mid-point formula to find the vertices of a triangle. According to midpoint formula, the coordinates of the midpoint of the line connecting the points $({x_1},{y_1})$ and $({x_2},{y_2})$is $\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$.
Then by mid-point formula for x coordinates of AB, we get,
$\dfrac{{{x_1} + {x_2}}}{2} = 0$
${x_1} + {x_2} = 0$
\[ \Rightarrow {x_1} = - {x_2}\] … (1)
Using mid-point formula for x coordinates of BC, we get,
$\dfrac{{{x_2} + {x_3}}}{2} = 5$
${x_2} + {x_3} = 10$
$ \Rightarrow {x_3} = 10 - {x_2}$ … (2)
Using mid-point formula for x coordinates of AC, we get
$\dfrac{{{x_1} + {x_3}}}{2} = 5$
$ \Rightarrow {x_1} + {x_3} = 10$ … (3)
Substituting (1) and (2) in (3), we get,
$
   - {x_2} + 10 - {x_2} = 10 \\
   \Rightarrow - 2{x_2} = 0 \\
   \Rightarrow {x_2} = 0 \\
 $
Substituting ${x_2} = 0$ in (1) and (2), we get,
\[{x_1} = - {x_2} = 0\]
${x_3} = 10 - {x_2} = 10 - 0 = 10$
Now we have the x coordinates of points A, B, and C.
Now we can take mid-point formula for y coordinates of AB,
$\dfrac{{{y_1} + {y_2}}}{2} = 12$
${y_1} + {y_2} = 24$
\[ \Rightarrow {y_1} = 24 - {y_2}\] … (4)
Using mid-point formula for y coordinates of BC, we get
$\dfrac{{{y_2} + {y_3}}}{2} = 0$
${y_2} + {y_3} = 0$
\[ \Rightarrow {y_3} = - {y_2}\] … (5)
Using mid-point formula for y coordinates of AC, we get
$\dfrac{{{y_1} + {y_3}}}{2} = 12$
$ \Rightarrow {y_1} + {y_3} = 24$ … (6)
Substituting (4) and (5) in (6), we get,
$
  {y_1} + {y_3} = 24 - {y_2} - {y_2} = 24 \\
   \Rightarrow - 2{y_2} = 0 \\
   \Rightarrow {y_2} = 0 \\
 $
Substituting ${y_2} = 0$ in (4) and (5), we get,
\[{y_1} = 24 - {y_2} = 24 - 0 = 24\]
\[{y_3} = - {y_2} = 0\]
Now we have the vertices of the triangle as A$(0,24)$, B$(0,0)$ and C$(10,0)$
Using distance formula,
\[
  A{B^2} = {\left( {{x_2} - {x_1}} \right)^2} + {\left( {{y_2} - {y_1}} \right)^2} \\
   = {\left( {0 - 0} \right)^2} + {\left( {24 - 0} \right)^2} \\
   = {24^2} \\
   = 576 \\
 \]
\[
  B{C^2} = {\left( {10 - 0} \right)^2} + {\left( {0 - 0} \right)^2} \\
   = {10^2} \\
   = 100 \\
 \]
$
  A{C^2} = {\left( {10 - 0} \right)^2} + {\left( {0 - 24} \right)^2} \\
   = {10^2} + {24^2} \\
   = 100 + 576 \\
   = 676 \\
 $
$
  A{B^2} + B{C^2} \\
   = 576 + 100 \\
   = 676 \\
   = A{C^2} \\
 $
As $A{B^2} + B{C^2} = A{C^2}$, by Pythagoras theorem, ABC is a right-angled triangle right angled at B.
The orthocenter of a right-angled triangle is the vertex on the right angle. So, the orthocenter of the triangle ABC is B $(0,0)$.
So, the correct option is option A.
Note: We can plot the given points as midpoints of a triangle for a better understanding of the question. We use the distance formula to get the square of the length of the sides and then verify Pythagoras theorem to confirm it is a right-angled triangle. We can also say that the triangle is right angles by checking the coordinates of the vertices. The orthocenter of a triangle is the point at which all the altitudes of the triangle intersects with each other. An altitude is a perpendicular line from one side of a triangle to the opposite vertex. For a right-angled triangle, the altitudes meet at the right-angled vertex and hence it is the orthocenter.