The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in one minute. [Use\[\pi ={}^{22}/{}_{7}\]]
A. \[5.72c{{m}^{2}}\]
B. \[8.01c{{m}^{2}}\]
C.\[10.26c{{m}^{2}}\]
D. \[13.13c{{m}^{2}}\]
Answer
Verified360.6k+ views
Hint:- Find the degree of the clock for 1 hour. Then find the degree of the clock for 1 minute. Use area of sector to find the area swept by a minute hand in 1 minute.
Complete step-by-step solution -
The minute hand of a clock completes a full circle degree in 1 hour. Consider the clock given below. The degree swept by the minute hand in 1 hour is \[{{360}^{\circ }}\] , i.e. the clock resembles circle and the degree of a circle is \[{{360}^{\circ }}\] . Thus it will be easier to remember that the degree swept by minute hand in 1 hour is \[{{360}^{\circ }}.\]
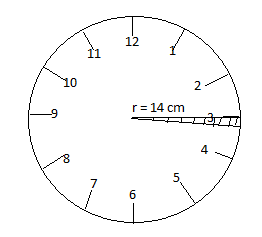
We know 1 hour = 60 minutes.
Degree swept by minute hand in 60 minutes = \[{{360}^{\circ }}\]
\[\therefore \]Degree swept by minute hand in 1 minute = \[\dfrac{360}{60}={{6}^{\circ }}\]
\[\therefore \]Degree swept by the minute hand in 1 minute is \[{{6}^{\circ }}\].
Hence, here \[\theta = {{6}^{\circ }}\]and radius r = 14 cm.
Now we need to find the area swept by the minute hand in 1 minute is equal to the shaded portion in the figure, which can be allocated as a sector. Hence we need to find the area of sector in the shaded region.
Area swept by minute hand = Area of sector.
We know, area of the sector,
\[\begin{align}
& = \dfrac{\theta }{360}\times \pi {{r}^{2}} \\
& = \dfrac{6}{360}\times \dfrac{22}{7}\times {{14}^{2}} \\
& = \dfrac{6}{360}\times \dfrac{22}{7}\times 14\times 14 \\
\end{align}\]
Cancel out the like terms and simplify it.
Area of sector
\[\dfrac{1}{60}\times 22\times 2\times 14\times =\dfrac{11\times 14\times 2}{30} = \dfrac{11\times 7\times 2}{15} = \dfrac{77\times 2}{15} = \dfrac{154}{15} = 10.267c{{m}^{2}}\]
\[\therefore \]Area of sector\[ = 10.267c{{m}^{2}}\]
\[\therefore \]Area swept by minute hand\[ = 10.267c{{m}^{2}}\]
Hence option C is the correct answer.
Note:- If we were asked to find the area swept in five minutes, then we first find the degree swept by 1 minute and then find the degree swept by 5 minutes.
Degree swept by 1 minute\[ = {{6}^{\circ }}\]
Degree swept by 5 minutes\[ = {{6}^{\circ }}\times 5={{30}^{\circ }}\]
So, area of sector\[ = \dfrac{30}{360}\times \pi {{r}^{2}} = 51.33c{{m}^{2}} = \]area swept by 5 minutes
Similarly, you can find areas swept by the minute hand for other time periods.
Complete step-by-step solution -
The minute hand of a clock completes a full circle degree in 1 hour. Consider the clock given below. The degree swept by the minute hand in 1 hour is \[{{360}^{\circ }}\] , i.e. the clock resembles circle and the degree of a circle is \[{{360}^{\circ }}\] . Thus it will be easier to remember that the degree swept by minute hand in 1 hour is \[{{360}^{\circ }}.\]
We know 1 hour = 60 minutes.
Degree swept by minute hand in 60 minutes = \[{{360}^{\circ }}\]
\[\therefore \]Degree swept by minute hand in 1 minute = \[\dfrac{360}{60}={{6}^{\circ }}\]
\[\therefore \]Degree swept by the minute hand in 1 minute is \[{{6}^{\circ }}\].
Hence, here \[\theta = {{6}^{\circ }}\]and radius r = 14 cm.
Now we need to find the area swept by the minute hand in 1 minute is equal to the shaded portion in the figure, which can be allocated as a sector. Hence we need to find the area of sector in the shaded region.
Area swept by minute hand = Area of sector.
We know, area of the sector,
\[\begin{align}
& = \dfrac{\theta }{360}\times \pi {{r}^{2}} \\
& = \dfrac{6}{360}\times \dfrac{22}{7}\times {{14}^{2}} \\
& = \dfrac{6}{360}\times \dfrac{22}{7}\times 14\times 14 \\
\end{align}\]
Cancel out the like terms and simplify it.
Area of sector
\[\dfrac{1}{60}\times 22\times 2\times 14\times =\dfrac{11\times 14\times 2}{30} = \dfrac{11\times 7\times 2}{15} = \dfrac{77\times 2}{15} = \dfrac{154}{15} = 10.267c{{m}^{2}}\]
\[\therefore \]Area of sector\[ = 10.267c{{m}^{2}}\]
\[\therefore \]Area swept by minute hand\[ = 10.267c{{m}^{2}}\]
Hence option C is the correct answer.
Note:- If we were asked to find the area swept in five minutes, then we first find the degree swept by 1 minute and then find the degree swept by 5 minutes.
Degree swept by 1 minute\[ = {{6}^{\circ }}\]
Degree swept by 5 minutes\[ = {{6}^{\circ }}\times 5={{30}^{\circ }}\]
So, area of sector\[ = \dfrac{30}{360}\times \pi {{r}^{2}} = 51.33c{{m}^{2}} = \]area swept by 5 minutes
Similarly, you can find areas swept by the minute hand for other time periods.
Last updated date: 25th Sep 2023
•
Total views: 360.6k
•
Views today: 5.60k
