Question

The length of a shadow of a tower on the plane ground is$\sqrt 3 $ times the height of the
 tower. The angle of elevation of sun is:
$A.{\text{ }}{45^ \circ }$
$B.{\text{ 3}}{0^ \circ }$
$C.{\text{ }}{60^ \circ }$
$D.{\text{ }}{90^ \circ }$

Answer 1

Hint- This question is solved by using $\tan \theta $.

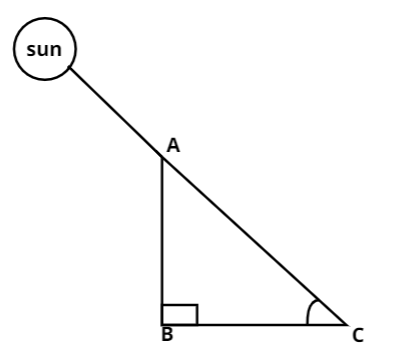
Now given that, the length of the shadow of a tower on the plane ground is $\sqrt 3 $ times the height of the tower.
Let the height of the tower be $AB$.
And the length of the shadow of the tower is $BC$ .
Therefore, the length of the shadow of the tower, $BC = \sqrt 3 AB$ .
Let the angle of elevation of the sun is $\theta $ ,
In right angled triangle $ABC$,
$
  tan\theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}} \\
  tan\theta = \dfrac{{AB}}{{BC}} \\
 $
Now putting the values of $BC$ we get,
$
  tan\theta = \dfrac{{AB}}{{\sqrt 3 AB}} \\
  or{\text{ }}tan\theta = \dfrac{1}{{\sqrt 3 }} \\
  or{\text{ }}\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }} \\
  {\text{or tan}}\theta {\text{ = tan3}}{0^ \circ } \\
  {\text{or }}\theta {\text{ = 3}}{0^ \circ } \\
 $
Hence, the angle of elevation of the sun is${30^ \circ }$ .
Thus, the correct option is $\left( B \right)$.
Note- When we face such types of questions firstly draw the figure and then analyze what we have to find like we did in this question. Here we firstly write the relation between length of tower and height of shadow of the tower and then use $\tan \theta $ from where we get the value of$\theta $ and hence we get our answer.