Question

The length of a rectangle is 10 feet less than 3 times its width. How do you find the dimensions of this rectangle if the area is 48 square feet?\[\]

Answer 1

Hint: We recall that if $l$ is the length and $b$ is the width of the rectangle then the area is given by $l\times b$. We assume width as $b=x$ feet and use the given data to have $l=3x-10$ feet. We equate the area $l\times b=x\left( 3x-10 \right)$ to given 48 square feet and solve for $x$ .\[\]

Complete step-by-step solution:
We know that a rectangle is a quadrilateral with sides perpendicular to each other. It has two types of sides: the greater side is called length denoted as $l$ and smaller side is called breadth or width denoted as $b$. The length and width together are called dimensions of the rectangle. The area of the rectangle is given by
\[A=l\times b\]
We are given the question that the length of a rectangle is 10 feet less than 3 times its width. Let us assume the width as $b=x$ feet then length will be 3 times width minus 10 that is $l=3\times b-10=3\times x-10=3x-10$ feet.

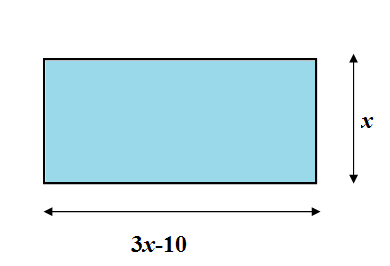
So the area of the rectangle is ;
\[A=l\times b=x\left( 3x-10 \right)\text{ square feet}\]
We are given this rectangle if the area is 48 square feet which means $A=48$. So we have
\[\begin{align}
  & 48=x\left( 3x-10 \right) \\
 & \Rightarrow 48=3{{x}^{2}}-10x \\
 & \Rightarrow 3{{x}^{2}}-10x-48=0 \\
\end{align}\]
We see that the above equation is a quadratic equation in $x$ which we shall solve by splitting the middle term method. We have
\[\begin{align}
  & \Rightarrow 3{{x}^{2}}-18x+8x-48=0 \\
 & \Rightarrow 3x\left( x-6 \right)+8\left( x-6 \right)=0 \\
 & \Rightarrow \left( x-6 \right)\left( 3x+8 \right)=0 \\
 & \Rightarrow x-6=0\text{ or }3x+8=0 \\
 & \Rightarrow x=6\text{ or }x=\dfrac{-8}{3} \\
\end{align}\]
We have two roots of the quadratic equation $x=6,\dfrac{-8}{3}$. Since the length of the line segment is always positive we reject the negative root $x=\dfrac{-8}{3}$ and accept $x=6$ as the only root. So the dimensions of the rectangle are
\[\begin{align}
  & b=x=6\text{ feet} \\
 & l=3x-10=3\left( 6 \right)-10=180=10=8\text{ feet} \\
\end{align}\]

Note: We should remember that area is measured in a unit that is square of unit of length. We can find the splitting terms of a quadratic equation $a{{x}^{2}}+bx+c=0$ by finding two numbers $p,q$ such that $p+q=-b,pq=c\times a$. We can prime factorize $c\times a$ get $p,q$. Here in this problem we prime factorize $48\times 3=2\times 2\times 2\times 2\times 3\times 3$ and select $p=-\left( 2\times 2\times 2 \right)=-8$ and $q=2\times 3\times 3=18$ to so split the term $-18$.