Question

The length, breadth and height of a room are 5m, 4m and 3m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of \[{\rm{Rs7}}{\rm{.50}}\] per \[{{\rm{m}}^2}\].

Answer 1

Hint: Here, we will find the area of the four walls of the cuboidal room along with the area of its rectangular ceiling by substituting the values of the dimensions of the given room. After finding the total area, we will multiply the cost of white washing \[1{{\rm{m}}^2}\] of a room by the total area to be covered by white washing.

Formula Used:
We will use the following formulas:
Area of four walls of a room \[ = 2h\left( {l + b} \right){{\rm{m}}^2}\], where \[h\] is the height , \[l\] is the length and \[b\] is the breadth of the wall.
Area of rectangular ceiling of a room \[ = \left( {l \times b} \right){{\rm{m}}^2}\], where \[l\] is the length and \[b\] is the breadth of the rectangle.

Complete step-by-step answer:
Let the length, breadth and height of the room be \[l,b\] and \[h\] respectively.

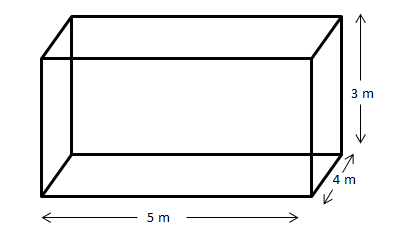
We will find the total area of the room by using the formula of area of four walls and ceiling of the room.
Therefore, we get
Total area of the four walls and the ceiling of the room \[ = 2h\left( {l + b} \right) + \left( {l \times b} \right){{\rm{m}}^2}\]……….\[\left( 1 \right)\]
Now, substituting \[l = 5\], \[b = 4\] and \[h = 3\] in the equation \[\left( 1 \right)\], we get
\[ \Rightarrow \] Total area of the four walls and the ceiling of the room \[ = 2\left( 3 \right)\left( {5 + 4} \right) + \left( {5 \times 4} \right)\]
Simplifying the expression, we get
\[ \Rightarrow \] Total area of the four walls and the ceiling of the room \[ = 6 \times 9 + 20\]
Multiplying the term, we get
\[ \Rightarrow \] Total area of the four walls and the ceiling of the room \[ = 54 + 20\]
Adding the terms, we get
\[ \Rightarrow \] Total area of the four walls and the ceiling of the room \[ = 74{{\rm{m}}^2}\]
Now, according to the question, it is given that the cost of white washing the walls of the room and the ceiling at the rate of \[{\rm{Rs7}}{\rm{.50}}\] per \[{{\rm{m}}^2}\].
Hence, the cost of white washing \[1{{\rm{m}}^2} = {\rm{Rs7}}{\rm{.50}}\]
Therefore, the cost of white washing \[74{{\rm{m}}^2}\] \[ = {\rm{Rs}}7.50 \times 74 = {\rm{Rs}}555\]

Then the cost of white washing the walls of the room and the ceiling at the rate of \[{\rm{Rs7}}{\rm{.50}}\] per \[{{\rm{m}}^2}\] is Rs. 555.
Therefore, this is the required answer.

Note:
Here the shape of the room is not given but we will assume it to be a cuboid because the dimensions of the room are given as length, breadth, and height. A cuboid is a three dimensional shape whose sides are rectangular. In real life, rooms are usually in the shape of a cuboid but if in case all the 4 walls and the top and bottom of a room have the same length, breadth, and height, this would mean that it is cubical in shape as a cube has all the sides equal and square shaped. Some other examples of cuboidal figures which we see in our day to day life are matchboxes, shoeboxes, books, etc. All of these have a length, breadth and height respectively.