Question

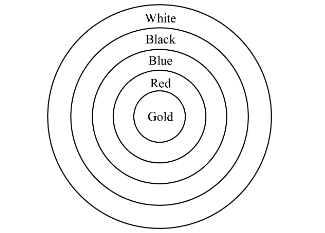
The figure depicts an archery target marked with its five scoring regions from the centre outwards as gold, red, blue, black and white. The diameter of the region representing the gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.

Answer 1

Hint: If the width of a band is added to the radius of the previous circle, then it gives the numerical value of the radius of the next concentric circle.
Use the formula $ A = \pi {r^2} $ to find the area of the circle.
Area of the scoring region can be calculated by taking the difference between the previous circle and the next circle.

Complete step-by-step answer:
Diameter of the gold circle is given as 21 cm.
Let $ {r_{gold}} $ be the radius of the gold circle.
 $
\Rightarrow {r_{gold}} = \dfrac{{21}}{2}\\
 = 10.5{\text{ cm}}
 $
The formula for the area of a circle is given by $ A = \pi r_{gold}^2 $
Area of the gold circle is given as
 $
\Rightarrow {A_{gold}} = \pi r_{gold}^2\\
 = \dfrac{{22}}{7}{\left( {10.5} \right)^2}\\
 = 346.5{\text{ c}}{{\text{m}}^2}
 $
We know that the width of the bands is 10.5 cm.
Now, we can find the radius of the next circle, i.e. red circle.
\[
\Rightarrow {\text{Radius of the red circle }} = {\text{ Radius of the gold circle }} + {\text{ Width of band}}\\
{\text{ = 10}}{\text{.5 + 10}}{\text{.5}}\\
{\text{ = 21 cm}}
\]
Sum of the area of the red and gold region can be calculated by using the formula $ \pi r_{_{red}}^2 $ .
 $
\Rightarrow {\text{Area of red and gold regions = }}\pi {\text{r}}_{red}^2\\
 = \pi {\left( {21} \right)^2}\\
 = \dfrac{{22}}{7}{\left( {21} \right)^2}\\
 = 1386{\text{ c}}{{\text{m}}^2}
 $
Area of the red region can be calculated by
\[
\left( {{\text{Sum of the areas of red, gold region}}} \right) - \left( {{\text{Area of gold region}}} \right){\text{ = 1386 - 346}}{\text{.5}}\;
\]
Area of the red region is $ {\text{1039}}{\text{.5 c}}{{\text{m}}^2} $ .
Now, we can calculate the radius of the blue circle by adding width to the radius of the red circle.
 \[
\Rightarrow {\text{Radius of the blue circle }} = {\text{ Radius of the red circle }} + {\text{ Width of band}}\\
{\text{ = 21 + 10}}{\text{.5}}\\
{\text{ = 31}}{\text{.5 cm}}
\]
Sum of the areas of the red, gold and blue region can be calculated by using the formula $ \pi r_{_{blue}}^2 $ .
 $
\Rightarrow {\text{Sum of the areas of blue, red, gold regions = }}\pi {\text{r}}_{blue}^2\\
 = \pi {\left( {31.5} \right)^2}\\
 = \dfrac{{22}}{7}{\left( {31.5} \right)^2}\\
 = 3118.5{\text{ c}}{{\text{m}}^2}
 $
 Area of the blue region can be calculated by
 $
\Rightarrow \left( {{\text{Sum of the areas of blue, red, gold regions}}} \right) - \left( {{\text{Sum of the areas of gold, red regions}}} \right){\text{ = 3118}}{\text{.5 - 1386}}\\
{\text{ = 1732}}{\text{.5 c}}{{\text{m}}^2}
 $
Now, we can find the radius of the next circle, i.e. black circle.
The radius of the black circle can be calculated by adding the radius of the blue circle to the width of the band.
\[
\Rightarrow {\text{Radius of the black circle }} = {\text{ Radius of the blue circle }} + {\text{ Width of band}}\\
{\text{ = 31}}{\text{.5 + 10}}{\text{.5}}\\
{\text{ = 42 cm}}
\]
Sum of the area of the red, gold, blue and black regions can be calculated by using the formula $ \pi r_{_{black}}^2 $ .
 $
\Rightarrow {\text{Sum of the areas of black, blue, red, gold regions = }}\pi {\text{r}}_{black}^2\\
 = \pi {\left( {42} \right)^2}\\
 = \dfrac{{22}}{7}{\left( {42} \right)^2}\\
 = 5544{\text{ c}}{{\text{m}}^2}
 $
Area of the black scoring region can be calculated by
\[
\Rightarrow \left( {{\text{Sum of the areas of black, blue, red and gold regions}}} \right){\text{ - }}\left( {{\text{Sum of the areas of blue, red and gold regions}}} \right){\text{ = 5544 - 3118}}{\text{.5}}\\
{\text{ = 2425}}{\text{.5 c}}{{\text{m}}^2}
\]
Now, we can find the radius of the next circle, i.e. white circle.
The radius of the white circle can be calculated by adding the radius of black circle to the width of the band.
\[
\Rightarrow {\text{Radius of the white circle }} = {\text{ Radius of the black circle }} + {\text{ Width of band}}\\
{\text{ = 42 + 10}}{\text{.5}}\\
{\text{ = 52}}{\text{.5 cm}}
\]
Sum of the area of the red, gold, blue, black and white regions can be calculated by using the formula $ \pi r_{_{white}}^2 $ .
 $
\Rightarrow {\text{Sum of the areas of white, black, blue, red, gold regions = }}\pi {\text{r}}_{white}^2\\
 = \pi {\left( {52.5} \right)^2}\\
 = \dfrac{{22}}{7}{\left( {52.5} \right)^2}\\
 = 8662.5{\text{ c}}{{\text{m}}^2}
 $
Area of the white scoring region can be calculated by
\[
\Rightarrow \left( {{\text{Sum of the areas of white, black, blue, red and gold region}}} \right){\text{ - }}\left( {{\text{Sum of the areas of black, blue, red and gold region}}} \right){\text{ = 8662}}{\text{.5 - 5544}}\\
{\text{ = 3118}}{\text{.5 c}}{{\text{m}}^2}
\]
Therefore, the areas of the gold, red, blue, black and white regions are \[{\text{346}}{\text{.5 c}}{{\text{m}}^2}\], \[{\text{1039}}{\text{.5 c}}{{\text{m}}^2}\], $ {\text{1732}}{\text{.5 c}}{{\text{m}}^2} $ , \[{\text{2425}}{\text{.5 c}}{{\text{m}}^2}\], \[{\text{3118}}{\text{.5 c}}{{\text{m}}^2}\] respectively.

Note: Students often make mistakes while calculating. To reduce the complications in finding the area of the circle the value of $\pi $ should be taken as $\dfrac{{22}}{7}$. In this type of question, students often use the value of diameter instead of radius in the formula $A = \pi {R^2}$, where $A$ denotes the area of the circle with radius $R$.