Question

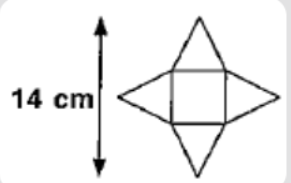
The figure below is the net of a prism made up of identical triangles, what is the total area of the prism if the side of the square is 6 cm.
[a] 75 sq-cm
[b] 84 sq-cm
[c] 95 sq-cm
[d] 56 sq-cm

Answer 1

Hint: Find the height of the triangles and use the fact that the area of a triangle $=\dfrac{1}{2}bh$ where b is the base and h is the height and the area of a square $={{a}^{2}}$. There are four triangles and one square. So, the net area will be the sum of 4 times the area of the triangle and area of the square.

Complete step-by-step answer:

Since the length of a side of square = 6cm.
We have AD = 6cm.
Also since the triangles are identical CG = HF
Since the total height of the diagram = 14.
We have CG+AD+HF = 14
i.e. CG+HF+6 = 14
i.e. 2CG+6 = 14
Subtracting 6 from both sides we get
2CG+6-6 = 14-6
i.e. 2CG = 8
Dividing both sides by 2 we get
CG = 4cm
Since CG = HF, we have
HF = 4 cm.
Now we know that the area of a triangle $=\dfrac{1}{2}bh$
Using we get the area of triangle ABC $=\dfrac{1}{2}\times AB\times CG=\dfrac{1}{2}\times 6\times 4=\dfrac{24}{2}=12$
Also, we know that the area of a square $={{a}^{2}}$
Using, we get the area of square ABED $=A{{D}^{2}}={{6}^{2}}=36$.
Hence the total area of the prism = 4 times the area of the triangle ABC + area of square ABED
$=4\times 12+36=48+36=84$
Hence the total area of faces of prism = 84 sq-cm.
Hence option [b] is correct.

Note: Although the figure above is referred to be of a prism, it is a pyramid. A pyramid has triangular faces, whereas a prism has rectangular faces. The diagram above is of a pyramid with a square base.
Further pyramids have only one base, whereas prisms have two.
A cone is an example of a pyramid with a circular base.