Question

The difference between the inside and outside surface of a cylindrical tube 14cm ling is 88sq.cm. if the volume of the tube is 176 cubic cm. find the inner diameter of the tube (in cm)

Answer 1

Hint: We will draw the diagram first from the given data to understand the problem. Then we are given the difference between the surfaces of the cylinder and the volume of the cylinder. We will consider the radius of the inner and outer cylinder as r and R respectively. The two data given will give two equations with the help of which we will find the value of radius and then the value of diameter.

Complete step-by-step answer:
Given that the solid shape is of a cylindrical pipe

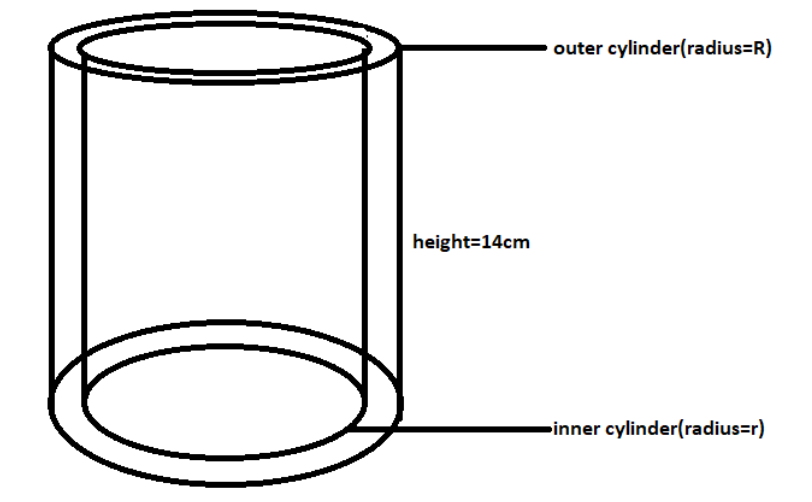
This is the diagrammatic explanation. The orange part is the volume of the cylindrical pipe.
Now we know that the lateral surface area of the cylinder is given by the formula \[2\pi rh\].
We are given the difference in surface area is 88sq.cm. We can write it as
\[2\pi Rh - 2\pi rh = 88\]
Taking \[2\pi h\] common,
\[2\pi h\left[ {R - r} \right] = 88\]
Substituting the value of \[\pi \]and h we get,
\[2 \times \dfrac{{22}}{7} \times 14\left[ {R - r} \right] = 88\]
On calculating we get,
\[2 \times 22 \times 2\left[ {R - r} \right] = 88\]
\[\left[ {R - r} \right] = 1\]……equation (I)
Now we are given that the volume of the tube is 176 cubic cm.
So we know that the volume of the tube is the difference between the volume of the outer tube and the volume of the inner tube.
So volume of tube is given by \[\pi {r^2}h\]
\[\pi h\left[ {{R^2} - {r^2}} \right] = 176\]
Substituting the values of \[\pi \] and h,
\[\dfrac{{22}}{7} \times 14\left[ {{R^2} - {r^2}} \right] = 176\]
On solving we get,
\[\left[ {{R^2} - {r^2}} \right] = 4\]
We can expand the LHS as,
\[\left( {R + r} \right)\left( {R - r} \right) = 4\]
But from equationI we can substitute one of the brackets as,
\[\left( {R + r} \right) = 4\]……equation (II)
Now on solving (adding) equation (I) and (II) we get,
\[2R = 5\]
Thus value of $R$ is
\[R = 2.5\]
To find the value of r we will use the equation above,
\[r = R - 1\]
Putting the values we get,
\[r = 2.5 - 1\]
\[r = 1.5\]
This is the radius of the inner cylinder pipe. Then the diameter of the same will be double the radius.
\[d = 2r = 2 \times 1.5 = 3\;cm\]
This is our required answer.
The inner diameter of the tube is 3 cm.


Note: Here note the key point in solving the problem is the equation we design. That is the difference in the surface areas and the volume of the cylinder. But we should know that the volume of the ring cylinder is formed. So we have removed the volume of the inner cylinder from the volume of the outer cylinder.
Also note that the dimension is specifically asked in cm. Here they have given all the dimensions already in cm but if not given be careful in that matter.