Question

The diameter of a metallic ball is $ 4.2cm $ . What is the mass of the ball, if the density of the metal is $ 8.9g\,per\,c{m^3} $ ?

Answer 1

Hint: A sphere is a geometrical object in three-dimensional space that is the surface of a ball. Like a circle in a two-dimensional space, a sphere is defined mathematically as the set of points that are all at the same distance r from a given point in a three-dimensional space. The sphere is three dimensional geometry. As we know that
 $ = \dfrac{4}{3}\pi {r^3} $
Where
r=radius of sphere
density of an object:
  $ \Rightarrow \rho = \dfrac{{mass}}{{volume}} $
We will first calculate Volume of an object and then calculate mass by using density formula.

Complete step by step solution:
Given,

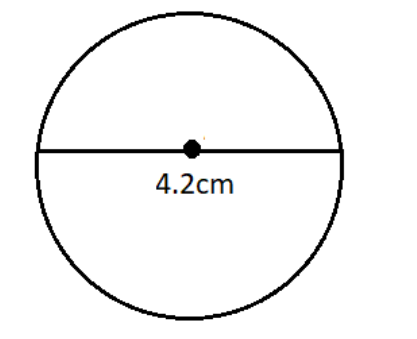
Diameter of sphere, $ d = 4.2\;cm $
$ r = \dfrac{d}{2} $
Radius of sphere, $ r = 2.1cm $
Density of metal, $ \rho = 8.9\;g/c{m^3} $
Volume of sphere, V=?
Mass of metal, M=?
As we know that
The volume of sphere is given by
 $ \Rightarrow V = \dfrac{4}{3}\pi {r^3} $
Put the value
 $ \Rightarrow V = \dfrac{4}{3}\pi {(2.1)^3} $
 $ \pi = \dfrac{{22}}{7} $
Simplify these
 $ \Rightarrow V = \dfrac{4}{3} \times \dfrac{{22}}{7} \times 2.1 \times 2.1 \times 2.1 $
 $ \Rightarrow V = 4 \times 22 \times 0.7 \times 0.3 \times 2.1 $
 $ \Rightarrow V = 38.808\;c{m^3} $
The volume of ball is $ 38.808\;c{m^3} $
As we know that
 $ \Rightarrow \rho = \dfrac{{mass}}{{volume}} $
Put the value
 $ \Rightarrow 8.9 = \dfrac{{mass}}{{38.808}} $
Simplify
 $ \Rightarrow mass = 8.9 \times 38.808 $
 $ \Rightarrow mass = 8.9 \times 38.808 $
 $ \Rightarrow mass = 345.39\;g $
Hence the mass of metal is $ 345.39\;g $
So, the correct answer is “ $ 345.39\;g $ ”.

Note: A sphere is symmetrical, round in shape. It is a three dimensional solid that has all its surface points at equal distances from the center. It has surface area and volume based on its radius. It does not have any faces, corners or edges.