Question

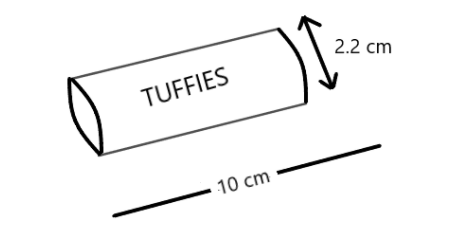
The diagram shows a tube containing chocolate sweets. Calculate the total surface area of the tube.

Answer 1

Hint: As we know that in the above question we have a tube, which is in the shape of a cylinder. We know the formula of the total surface area of the cylinder is $ 2\pi r(h + r) $ . In this question we have been given height i.e. $ h = 10 $ and the diameter is given. If we look at the top or the bottom of the cylindrical tube we can see that it is a circular shape. So we can see that in the figure we have been given the full length i.e. diameter of the circle. So we will calculate the radius i.e. $ r $ from this and then apply the formula.

Complete step by step solution:
From the figure we can see that we have been given the diameter , so we can find the radius i.e. $ r = \dfrac{d}{2} $ . So we have the value
 $ r = \dfrac{{2.2}}{2} = 1.1 $ .
Now we know the formula of the total surface area of the cylinder i.e.
 $ 2\pi r(h + r) $ .
We have $ r = 1.1 $ and $ h = 10 $ .
Now by putting the values we have
 $ 2 \times \dfrac{{22}}{7} \times 1.1(10 + 1.1) $ . Now we will solve this, $ 6.914(11.1) $ .
On further solving we have the value $ 76.74 $ .
Hence the required Total surface area is $ 76.74c{m^2} $ .
So, the correct answer is “ $ 76.74\;c{m^2} $ ”.

Note: We should note that there are two circular area in the top and the bottom of the cylinder, so their area is $ \pi {r^2} + \pi {r^2} = 2\pi {r^2} $ , since there are two circles. After that if we unfold a cylinder open on both sides, then we obtain a rectangle. We should note that the area of the rectangle is the product of two sides i.e. one side is the height of the tube and the other side is the perimeter of the circle. So we can write the area of the rectangle is $ 2r\pi \times h = 2\pi rh $ . So this gives us the total surface area of the cylinder i.e. $ 2\pi {r^2} + 2\pi rh = 2\pi r(r + h) $ .