Question

The diagonals of a quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus? Draw a rough figure to justify your answer.

Answer 1

Hint: First, we will use the mid point theorem where the line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side. Apply this theorem, and then use the given conditions to find the required value.

Complete step-by-step answer:
It is given that ABCD is a quadrilateral and its diagonals are perpendicular with each other.
We will now plot the mid points of the sides of the quadrilateral ABCD with PQRS and join them.

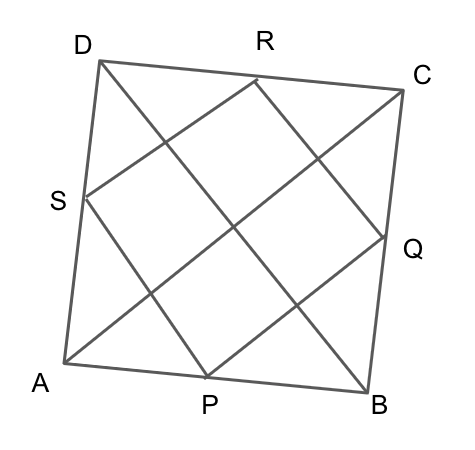
First, we will take the triangle \[\Delta {\text{ABC}}\] where P and Q are mid points of AB and BC.
We know that in the mid point theorem, the line segment in some triangle ABC joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.

So using the mid point theorem we know that the length AC and PQ are perpendicular with each other.
\[\therefore {\text{PQ||AC and PQ = }}\dfrac{1}{2}{\text{AC ......}}\left( 1 \right)\]
We will now take the triangle \[\Delta {\text{ACD}}\] where R and S are mid points of CD and AD.
So using the mid point theorem we know that the length SR and AC are perpendicular with each other.
\[\therefore {\text{SR||AC and SR = }}\dfrac{1}{2}{\text{AC ......}}\left( 2 \right)\]
From equation \[\left( 1 \right)\] and equation \[\left( 2 \right)\], we get
\[{\text{PQ||SR}}\] and \[{\text{PQ = SR}}\]

Thus, PQRS is a rectangle.

Note: In this question, students should know that opposite sides of the rectangle are equal and parallel. Students must crack the point of using the mid point theorem, the line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side. If we are able to crack this point, then the proof is very simple.