Question

The CSA of a right circular cylinder of height \[14{\text{ cm}}\] is \[{\text{88 c}}{{\text{m}}^2}\]. Find the radius of the base of the cylinder.

Answer 1

Hint: Here we will use the formula of CSA (Curved surface area) of the cylinder for calculating the radius of the cylinder which equals to as below:
\[{\text{Curved surface area}} = 2\pi rh\]
Where \[r\] is known as the radius of the base of the cylinder, \[h\] is the height of the cylinder.

Complete step-by-step solution:
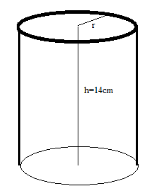
Step 1: From the below diagram we can see that the height of the cylinder is given which is \[14{\text{ cm}}\] and \[r\] is the radius of the base of the cylinder.
\[{\text{Curved surface area}} = 88{\text{ c}}{{\text{m}}^2}\]

Step 2: Now, by using the formula of the curved surface area of the cylinder and by substituting the values of \[h = 14{\text{ cm}}\]and \[\pi = \dfrac{{22}}{7}\] , and \[{\text{Curved surface area}} = 88{\text{ c}}{{\text{m}}^2}\], we get:
\[88{\text{ c}}{{\text{m}}^2} = 2 \times \dfrac{{22}}{7} \times r \times 14{\text{ cm}}\] ……………. (1)
By dividing \[14\] with \[7\] into the RHS side of the expression (1), we get:
\[ \Rightarrow 88{\text{ c}}{{\text{m}}^2} = 2 \times 22 \times r \times 2{\text{ cm}}\]
By bringing all the terms of the RHS side into the LHS side in the expression \[88 = 2 \times 22 \times r \times 2\] , we get:
\[ \Rightarrow \dfrac{{88{\text{ c}}{{\text{m}}^2}}}{{2 \times 22 \times 2{\text{ cm}}}} = r\]
By dividing into the LHS side we get:
\[ \Rightarrow 1{\text{ cm}} = r\]

\[\therefore \] The radius of the base of the cylinder is equal to \[1{\text{ cm}}\]

Note: Students need to remember some basic formulas for finding surface areas of the cylinder because there are two types of area, one is a Curved surface area and the second is the Total surface area. The formulas for finding both is given below:
\[{\text{Curved surface area}} = 2\pi rh\]
The total surface area of the cylinder\[ = 2\pi r\left( {r + h} \right)\], where \[r\] is known as the radius of the base of the cylinder, \[h\] is the height of the cylinder.
Similarly, the formula for finding the volume of the cylinder is as below:
\[{\text{Volume of the cylinder}} = \pi {r^2}h\]