The coach of a cricket team buys 3 bats and 6 balls for Rs 3900. Later, she buys another bat and 3 more balls of the same kind for Rs 1300. Represent this situation algebraically and geometrically.
Answer
Verified361.5k+ views
Hint: We make use of algebraic equations by representing the price of bats as x and price of balls as y. Then, we make use of the conditions in the question to get two algebraic equations in terms of x and y. Finally, we solve these equations to get the value of x and y.
Complete step-by-step solution:
Since, we have represented the price of the bats as x and price of the balls as y. We can now start applying the conditions given in the question. Firstly, we have that the coach of a cricket team buys 3 bats and 6 balls for Rs 3900. This condition gives us-
3x + 6y = 3900 -- (1)
(Since, the number of bats are 3, the total price of the bats is 3x. Further, the number of balls is 6, the total price of the balls is 6y)
Now, using the second condition, the total price of buying another bat and 3 more balls of the same kind is Rs 1300. Thus, we have-
x + 3y = 1300 -- (2)
Now, we have to solve (1) and (2) to get the value of x and y. To do so, we multiply equation (2) by 3 and then subtract (1) from (2). Thus, we have,
3(x+3y) – (3x+6y) = 3900 – 3900
3x+9y – (3x+6y) = 0
3y = 0
y=0
Now, we put this value of y in (2), we have,
x + (3$\times $0) = 1300
x = 1300
Thus, the price of the bat (which was x) is Rs 1300 and the price of the ball (which was y) is Rs 0.
To represent this graphically,
We can take various points like x=0,100,200 and other values and plug it in (1) and (2) separately. For example, for equation (1),
3x+6y=3900
y= $\dfrac{3900-3x}{6}$ -- (A)
We put, x=0,100 and 200
We get y=650, 600 and 550 respectively (from plugging value of x in (A) )
Then we can get, three points,
(0,650), (100,600) and (200,550)
One can now plot these points and make a line through them to get the desired line graphically.
Similarly, we do for equation (2),
x+3y=1300
y=$\dfrac{1300-x}{3}$ -- (B)
We put, x=0,100 and 200
We get y=433.33, 400 and 366.67 respectively (from plugging value of x in (B))
Then we can get, three points-
(0,433.33), (100,400) and (200,366.67)
One can now plot these points and make a line through them to get the desired line graphically.
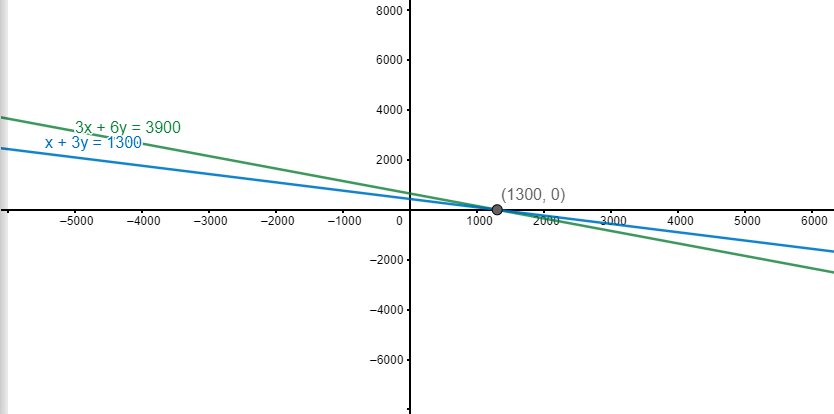
Correspondingly, we will get different values of y corresponding to x. With this information, we can get various (x,y) coordinates for (1) and (2). Thus, we can then plot those points and join them by the corresponding lines for (1) and (2). This has been shown on the graph above.
Hence, the equations (1) and (2) represent the situation algebraically. Further, this has been done graphically.
Note: In problems involving word problems, the first step should be to understand the problem in terms of algebraic variables. This would then help in representing the problems in terms of these algebraic variables, which would ultimately help in solving the problem mathematically as done in this case. For representing on the graph, although in the solution we have found three pairs of points, one needs to find only two pairs of coordinates for the respective line equation to eventually plot them and draw a line through them. This would help in reducing the time for solving the problem.
Complete step-by-step solution:
Since, we have represented the price of the bats as x and price of the balls as y. We can now start applying the conditions given in the question. Firstly, we have that the coach of a cricket team buys 3 bats and 6 balls for Rs 3900. This condition gives us-
3x + 6y = 3900 -- (1)
(Since, the number of bats are 3, the total price of the bats is 3x. Further, the number of balls is 6, the total price of the balls is 6y)
Now, using the second condition, the total price of buying another bat and 3 more balls of the same kind is Rs 1300. Thus, we have-
x + 3y = 1300 -- (2)
Now, we have to solve (1) and (2) to get the value of x and y. To do so, we multiply equation (2) by 3 and then subtract (1) from (2). Thus, we have,
3(x+3y) – (3x+6y) = 3900 – 3900
3x+9y – (3x+6y) = 0
3y = 0
y=0
Now, we put this value of y in (2), we have,
x + (3$\times $0) = 1300
x = 1300
Thus, the price of the bat (which was x) is Rs 1300 and the price of the ball (which was y) is Rs 0.
To represent this graphically,
We can take various points like x=0,100,200 and other values and plug it in (1) and (2) separately. For example, for equation (1),
3x+6y=3900
y= $\dfrac{3900-3x}{6}$ -- (A)
We put, x=0,100 and 200
We get y=650, 600 and 550 respectively (from plugging value of x in (A) )
Then we can get, three points,
(0,650), (100,600) and (200,550)
One can now plot these points and make a line through them to get the desired line graphically.
Similarly, we do for equation (2),
x+3y=1300
y=$\dfrac{1300-x}{3}$ -- (B)
We put, x=0,100 and 200
We get y=433.33, 400 and 366.67 respectively (from plugging value of x in (B))
Then we can get, three points-
(0,433.33), (100,400) and (200,366.67)
One can now plot these points and make a line through them to get the desired line graphically.
Correspondingly, we will get different values of y corresponding to x. With this information, we can get various (x,y) coordinates for (1) and (2). Thus, we can then plot those points and join them by the corresponding lines for (1) and (2). This has been shown on the graph above.
Hence, the equations (1) and (2) represent the situation algebraically. Further, this has been done graphically.
Note: In problems involving word problems, the first step should be to understand the problem in terms of algebraic variables. This would then help in representing the problems in terms of these algebraic variables, which would ultimately help in solving the problem mathematically as done in this case. For representing on the graph, although in the solution we have found three pairs of points, one needs to find only two pairs of coordinates for the respective line equation to eventually plot them and draw a line through them. This would help in reducing the time for solving the problem.
Last updated date: 22nd Sep 2023
•
Total views: 361.5k
•
Views today: 8.61k
