Question

The circumcentre of the triangle with vertices (0, 0), (3, 0) and (0, 4) is?
(a) (1, 1)
(b) $ \left( 2,\dfrac{3}{2} \right) $
(c) $ \left( \dfrac{3}{2},2 \right) $
(d) None of these

Answer 1

Hint: First, before proceeding for this, we must draw the triangle in the graph so that we get to know what this triangle looks like. Then, we should be aware of the fact that in a right angled triangle, the value of the circumcentre of the triangle is the midpoint of the hypotenuse. Then, by using midpoint formula for the points $ \left( {{x}_{1}},{{y}_{1}} \right) $ and $ \left( {{x}_{2}},{{y}_{2}} \right) $ as $ x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2},y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2} $ , we get the desired answer.

Complete step-by-step answer:
In this question, we are supposed to find the circumcentre of the triangle with vertices (0, 0), (3, 0) and (0, 4).
So, before proceeding for this, we must draw the triangle in the graph so that we get to know what this triangle looks like.

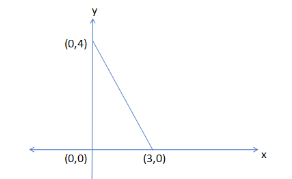
So, we can clearly see from the figure that the graph of the triangle with vertices (0, 0), (3, 0) and (0, 4) is a right angled triangle.
Now, we should be aware of the fact that in a right angled triangle, the value of the circumcentre of the triangle is the midpoint of the hypotenuse.
Now, we need to use the midpoint formula to calculate the circumcentre of the given triangle.
So, midpoint formula for the points $ \left( {{x}_{1}},{{y}_{1}} \right) $ and $ \left( {{x}_{2}},{{y}_{2}} \right) $ are given by:
 $ x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2},y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2} $
So, now the points $ \left( {{x}_{1}},{{y}_{1}} \right) $ from the figure is (3, 0) and points $ \left( {{x}_{2}},{{y}_{2}} \right) $ is (0, 4).
Then, by using the values of the above points, we get the coordinates of the midpoint of hypotenuse of the triangle as:
 $ x=\dfrac{3+0}{2},y=\dfrac{0+4}{2} $
Then, solve the above expression to get the value of coordinates as:
 $ \begin{align}
  & x=\dfrac{3}{2},y=\dfrac{4}{2} \\
 & \Rightarrow x=\dfrac{3}{2},y=2 \\
\end{align} $
So, the values of the midpoints of the hypotenuse is $ \left( \dfrac{3}{2},2 \right) $ which is also the value of circumcentre of the right angled triangle with vertices as (0, 0), (3, 0) and (0, 4).
So, the correct answer is “Option C”.

Note: Now, to solve these types of questions we need to be careful with the coordinates as the first coordinate is always x coordinate and second coordinate is always y-coordinate. If we confuse between them and select y as first coordinate then we get our answer as option (b) which is a wrong answer. So, we must be careful about the coordinate system.