Question

The central angle of a semicircle is:
A. ${{90}^{\circ }}$
B. ${{270}^{\circ }}$
C. ${{180}^{\circ }}$
D. ${{360}^{\circ }}$

Answer 1

Hint: For solving this question you should know about the figure and area of a semicircle. A complete circle contains two semicircles in it. And we can prove it by an example. And then we can also find that the central angle of a semicircle is exactly half of the centre of a circle. So, for this we will prove the half area.

Complete step by step answer:
According to our question it is asked of us to find the central angle of a semicircle. So, if we take a circle with a radius of 7m and we see the diagram for this, then:

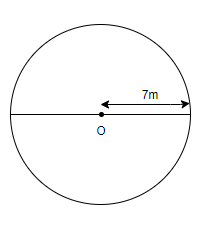
The circle’s centre is a point where the angle is ${{360}^{\circ }}$. But if we see a semicircle, then:

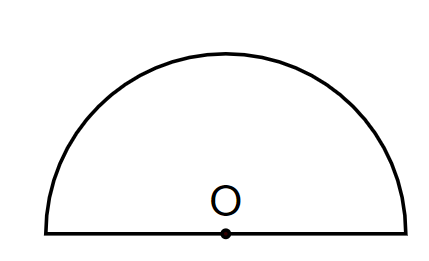
Here the centre is on a straight line and the angle on any point of a straight line is always ${{180}^{\circ }}$. So, the angle is ${{180}^{\circ }}$. And if we look for the areas of semicircle and circle, then:
It is given that the radius of the circle is 7m. So, we know that the area of a circle is calculated by $\pi {{r}^{2}}$.
Thus the area of a whole circle is:
$\begin{align}
  & A=\pi {{\left( 7 \right)}^{2}} \\
 & \Rightarrow A=49\pi \\
 & \Rightarrow A=49\times \dfrac{22}{7} \\
 & \Rightarrow A=154{{m}^{2}} \\
\end{align}$
So, the area of the whole circle is $154{{m}^{2}}$.
We know that, to calculate the area of a semicircle, it is half of the whole circle. So, we can calculate it by the formula $\dfrac{1}{2}\pi {{r}^{2}}$. The radius for the semicircle is 7m.
So, the area of the semicircle is:
$\begin{align}
  & A'=\dfrac{1}{2}\pi {{r}^{2}} \\
 & \Rightarrow A'=\dfrac{1}{2}\times \pi \times {{\left( 7 \right)}^{2}} \\
 & \Rightarrow A'=77{{m}^{2}} \\
\end{align}$
So, the area of the semicircle is exactly half of the whole circle and it is $77{{m}^{2}}$.
So, the correct answer is “Option C”.

Note: The area of a semicircle is half the area of a circle of the same radius and a circle contains two semicircles in its area. We can directly do half of the complete area of the circle to calculate the area of a semicircle. And it is mandatory that the area will be of the same radius circle and semicircle of same radius.