Question

The block A is kept over plank B. The maximum horizontal acceleration of the system in order to prevent slipping of A over B is $a=2m{{s}^{-2}}.$ Find the coefficient of friction between A and B.

Answer 1

Hint: To solve this kind of problem, the first step is always making the free body diagram. The force body diagram is to be made for body A. The frictional force is given by \[\mu N\]. Comparing the forces acting against each other will solve the problem.

Step by step solution:
Let’s start by making a free body diagram of the problem.

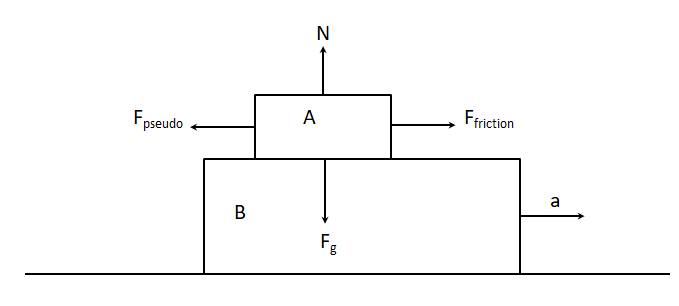
Here, we only need to make the free body diagram for block A, since the problem needs us to only find the coefficient of friction \[(\mu )\], between the block A and the plank B.
Let the mass of the block A be m. The acceleration due to gravity (g), acting downwards on the block. Hence, the downward force is ${{F}_{g}}=mg$. The normal force acting on the block A acts perpendicular to the block A, hence, vertically opposite to the force \[{{F}_{g}}\]. The maximum possible acceleration of plank B is a, that is, $a=2m{{s}^{-2}}.$ This causes a pseudo backward force on the block A. Hence, in the free body diagram, the pseudo force \[{{F}_{pseudo}}\] acts on the block A towards the opposite direction of the movement of plank B. This causes the frictional force to act in the opposite direction to that of the movement of pseudo force. Hence, frictional force $({{F}_{friction}})$ acts towards the right of block A.

Now equating the forces along the vertical axis, we get, N=mg. Now, upon equating the forces along the horizontal axis we get, \[{{F}_{pseudo}}={{F}_{friction}}\]. We know that the frictional force is given by, \[{{F}_{friction}}=\mu N\Rightarrow {{F}_{friction}}=mg\mu \]. The pseudo force acting on the block A is, \[{{F}_{pseudo}}=ma=2m\]. Equating these two we get, $mg\mu =2m\Rightarrow \mu g=2\Rightarrow \mu =\dfrac{2}{g}$. Hence, the coefficient of friction between the block A and the plank B is $\mu =\dfrac{2}{g}$.

Note:
In this problem, the pseudo force can be thought of as the inertial force. To picture it, let’s consider the example of a bus journey. When we are standing in a bus, as soon as the bus starts to move with a slightly large acceleration, we feel a jerk pushing us backward. This backward jerk is known as the pseudo force acting on the block A.