Question

The base of a triangle is divided into three equal parts. If \[{t_1},{t_2},{t_3}\] are the tangents of the angles subtended by these parts at the opposite vertex, prove that\[\left( {\dfrac{1}{{{t_1}}} + \dfrac{1}{{{t_2}}}} \right)\left( {\dfrac{1}{{{t_2}}} + \dfrac{1}{{{t_3}}}} \right) = 4\left( {1 + \dfrac{1}{{{t_2}^2}}} \right)\].

Answer 1

Hint: To solve this question, we first make two lines from vertex to the base such that they divide it into three equal parts. Then we apply \[m:n\] rule in any two of the triangles thus formed. In this way we get two equations. We will divide them. Then we simplify it further to reach the given equation.
Formula used: If \[\alpha \] and \[\beta \] are any two angles, then cot function of their sum is given as
\[cot(\alpha + \beta ) = \dfrac{{\cot \alpha \cot \beta - 1}}{{cot\beta + cot\alpha }}\].
According to m-n theorem if \[m\] and \[n\] are the length of base of two triangles and \[\alpha \] and \[\beta \] are the angles of vertex, then
\[\left( {m{\text{ }} + {\text{ }}n} \right)cot\theta = mcot\alpha-ncot{\beta} \]

Complete step-by-step solution:

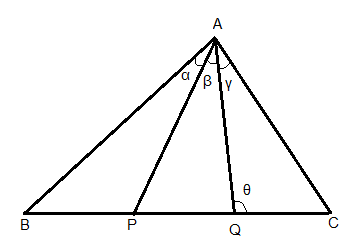
First we construct the diagram according to the question. Here P and Q divide the base in three equal parts \[BP = PQ = QC = x\]
And \[\angle BAP = \alpha \], \[\angle PAQ = \beta \] and \[\angle QAC = \gamma \]
Now, from the question, \[tan\alpha = {t_1},tan\beta = {t_2},tan\gamma = {t_3}\]
Now according to m-n theorem if \[m\] and \[n\] are the length of base of two triangles and \[\alpha \] and \[\beta \] are the angles of vertex, then
\[\left( {m{\text{ }} + {\text{ }}n} \right)cot\theta = mcot\alpha -ncot{\beta} \]
Using this, we get,
\[\Delta ABC\] we get \[(2x + x)cot\theta = 2xcot(\alpha + \beta ) - xcot\gamma \,\,\,\, \to (1)\]
\[\Delta APC\] we get \[(x + x)cot\theta = xcot\beta - xcot\gamma \,\,\, \to (2)\]
We will now divide equation \[(1)\] and\[(2)\],
\[
  \dfrac{{(2x + x)cot\theta }}{{(x + x)cot\theta }} = \dfrac{{2xcot(\alpha + \beta ) - xcot\gamma }}{{xcot\beta - xcot\gamma }} \\
   \Rightarrow \dfrac{{3x\cot \theta }}{{2x\cot \theta }} = \dfrac{{x(2cot(\alpha + \beta ) - cot\gamma )}}{{x(cot\beta - cot\gamma )}} \\
   \Rightarrow \dfrac{3}{2} = \dfrac{{(2cot(\alpha + \beta ) - cot\gamma )}}{{(cot\beta - cot\gamma )}} \\
   \Rightarrow 3(cot\beta - cot\gamma ) = 2 \times (2cot(\alpha + \beta ) - cot\gamma ) \\
   \Rightarrow 3cot\beta - 3cot\gamma = 4cot(\alpha + \beta ) - 2cot\gamma \]
We know that \[cot(\alpha + \beta ) = \dfrac{{\cot \alpha \cot \beta - 1}}{{cot\beta + cot\alpha }}\], using this we get,
\[
   \Rightarrow 3cot\beta - 3cot\gamma + 2cot\gamma = 4\left( {\dfrac{{\cot \alpha \cot \beta - 1}}{{\cot \beta + \cot \alpha }}} \right) \\
 \Rightarrow 3cot\beta - cot\gamma = 4\left( {\dfrac{{\cot \alpha \cot \beta - 1}}{{\cot \beta + \cot \alpha }}} \right) \\
   \Rightarrow (\cot \beta + \cot \alpha )(3cot\beta - cot\gamma ) = 4\cot \alpha \cot \beta - 4 \\
   \Rightarrow 3{\cot ^2}\beta - \cot \beta cot\gamma + 3\cot \alpha cot\beta - \cot \alpha cot\gamma = 4\cot \alpha \cot \beta - 4 \\
   \Rightarrow 3{\cot ^2}\beta + 4 = 4\cot \alpha \cot \beta + \cot \beta cot\gamma - 3\cot \alpha cot\beta + \cot \alpha cot\gamma \]
We add \[{\cot ^2}\beta \] on both LHS and RHS,
\[
   \Rightarrow 3{\cot ^2}\beta + 4 + {\cot ^2}\beta = \cot \alpha \cot \beta + \cot \beta cot\gamma + \cot \alpha cot\gamma + {\cot ^2}\beta \\
   \Rightarrow 4 + 4co{t^2}\beta = co{t^2}\beta + cot\alpha \cdot cot\beta + cot\beta cot\gamma + cot\gamma \cdot cot\alpha \\
   \Rightarrow 4(1 + co{t^2}\beta ) = (cot\beta + cot\alpha )(cot\beta + cot\gamma ) \]
As \[tan\alpha = {t_1},tan\beta = {t_2},tan\gamma = {t_3}\]
We say \[\cot \alpha = \dfrac{1}{{{t_1}}},\cot \beta = \dfrac{1}{{{t_2}}},\cot \gamma = \dfrac{1}{{{t_3}}}\]
Putting this value in above given step, we get
\[ \Rightarrow 4\left( {1 + \dfrac{1}{{{t_2}^2}}} \right) = \left( {\dfrac{1}{{{t_1}}} + \dfrac{1}{{{t_2}}}} \right)\left( {\dfrac{1}{{{t_2}}} + \dfrac{1}{{{t_3}}}} \right)\]
Hence here we have proved the required.

Note: We have to be very careful while drawing the diagram as our whole solution is based on it. We also have to be careful while doing the calculation as it is lengthy and there are great chances of us missing out any term. The above formulas must be learnt as they make such problems easy to solve.