Question

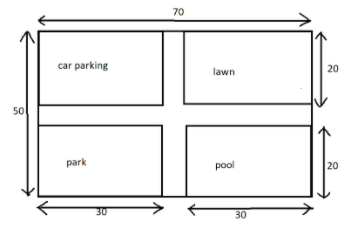
The area of car parking, lawn, swimming pool and the park is the same. Find the area of the remaining portion shown in the figure.
All the dimensions are in m.

Answer 1

Hint: We have to calculate the area of the remaining portion shown in the above figure. Firstly find the area of whole field whose dimension is \[70m \times 50m\], then calculate the area of the portion covered by either park, lawn, pool or car parking then simply multiply the area obtained by four as it is given that the area of all figure is same or separately calculate their area and then add. Then to find the area of the remaining uncovered portion subtract their total area from the area of the field whose dimension is \[70m \times 50m\].

Complete step-by-step solution:
Given that the dimension of the field is \[70m \times 50m\].
We know that the area of the rectangular field $ = length \times breadth$
So, the area of the field $ = 70m \times 50m = 3500{m^2}$
Now, we have to calculate the area of either park, pool, lawn or car parking.
Area of rectangular lawn $ = 30m \times 20m = 600{m^2}$.
It is given that the area of car parking, lawn, pool and park are equal. So, the total covered area is four times the area of the lawn.
So, total covered area $ = 4 \times 600{m^2} = 2400{m^2}$
Now, the area of the remaining portion $ = 3500{m^2} - 2400{m^2} = 1100{m^2}$.

Thus, we obtained the area of the remaining portion of the field as $1100{m^2}$.

Note: Area of any closed figure is always expressed in square units.
This can be alternatively solved by
We can get the dimension of the remaining horizontal portion simply by studying the figure which is $70m \times 10m$ and similarly the dimension of the vertical portion is $10m \times 50m$. Then find their total area. Since the area at the intersection of horizontal and vertical portion is added twice, find the area of intersection and subtract it from the total area to get the required area.