Question

The aperture of a camera is formed by 10 blades overlapping to from a regular decagon. What is the measure of \[\angle BAX?\].

A.\[{45^ \circ }\]
B.\[{36^ \circ }\]
C.\[{144^ \circ }\]
D.\[{44^ \circ }\]

Answer 1

Hint: In this question we have given it is a decagon. So clearly it has 10 sides. So using the formula for the sum of interior angles of \[n - \]sided polygon we will get the sum of angles. After that using the formula for calculating each interior angle of a polygon \[ = \] \[\dfrac{{\left( {n - 2} \right)180}}{n};\] where n is the number of sides of polygon.
We will get measure of each interior angle. Then using the formula: exterior angle \[ = \]\[{180^ \circ } - \] interior angle we will get the required answer.

Complete step-by-step answer:

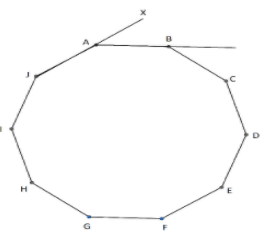
We have given the aperture of a camera is formed by 10 blades overlap to form a regular decagon.
As we know the sum of interior angles of \[n - \]sided polygon \[ = \] \[\left( {n - 2} \right) \times 180\].
Here, we have decagon
So, \[n = 10\]
Hence, sum of interior angles of decagon \[ = \left( {10 - 2} \right) \times {180^ \circ }\] \[ = 8 \times {180^ \circ }\]
\[ \Rightarrow \]Sum of angles of interior angles of decagon\[ = {1440^ \circ }\]
Now, using the formula for calculating each interior angle of a polygon \[ = \] \[\dfrac{{\left( {n - 2} \right)180}}{n};\] where n is the number of sides of polygon.
Here, \[n = 10\] so we get,
Each interior angle of a decagon \[ = \] \[\dfrac{{\left( {10 - 2} \right)180}}{{10}}\]
\[ \Rightarrow \dfrac{{8 \times 180}}{{10}}\] \[ = 8 \times 18\]
\[ \Rightarrow {144^ \circ }\]
Hence, we get each interior angle of a decagon is of\[{144^ \circ }\].
So, from the figure we can say that \[\angle JAB = {144^ \circ }\]
Now,
Use the fact that, exterior angle \[ = \]\[{180^ \circ } - \] interior angle
Here, we have\[\angle JAB = {144^ \circ }\]
 Therefore, exterior angle of a decagon \[ = {180^ \circ } - {144^ \circ }\]
     \[ = {36^ \circ }\]
From the figure we can say that \[\angle BAX\]is an exterior angle.
\[\therefore \angle BAX = {36^ \circ }\]
Thus, the measure of \[\angle BAX\] is \[{36^ \circ }\]
Hence, option B. \[{36^ \circ }\]is the correct answer.

Note: Interior angle of a polygon is an angle inside a polygon at a vertex of the polygon.
Exterior angle of a polygon is an angle at a vertex of the polygon, outside the polygon, formed by one side and the extension of an adjacent side.
The sum of exterior angles of a polygon must be \[{360^ \circ }\].