Question

The angle of elevation of an aeroplane from a point on the ground is ${60^0}$. After a flight of 30 seconds the angle of elevation becomes ${30^0}$ . If the aeroplane is flying at a constant height of $3000\sqrt 3 {\text{ }}m$. Find the speed of the aeroplane.

Answer 1

Hint- Use the definition of angle of elevation and simple formula of tangent, and then proceed further by using the basic formula of speed as distance upon time.

Complete step-by-step answer:

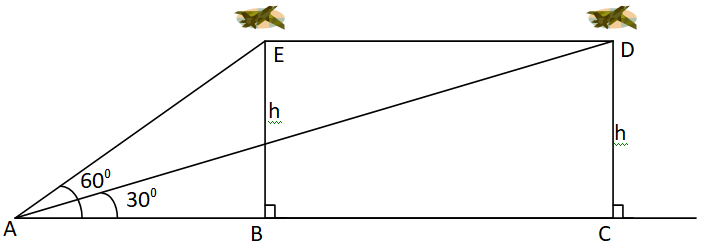
We will use the above diagram to solve the problem.
Let $E{\text{ and }}D$ be the two positions of the plane and $A$ be the point of observation.
Let $ABC$ be the horizontal line through $A$ .
It is given that angles of elevation of the plane in two positions $E{\text{ and }}D$ from the point $A$ are ${\text{6}}{{\text{0}}^0}{\text{ and 3}}{{\text{0}}^0}$ respectively.
\[\angle EAB = {60^0},\angle DAB = {30^0}\]
It is also given that $EB = DC = 3000\sqrt 3 {\text{ }}m$
As we know that in any right angled triangle $\tan \theta = \dfrac{{{\text{height }}}}{{{\text{base}}}}$
$
  \therefore {\text{ In }}\Delta ABE,\tan \left( {\angle EAB} \right) = \dfrac{{BE}}{{AB}} \\
   \Rightarrow \tan \left( {{{60}^0}} \right) = \dfrac{h}{{AB}} \\
   \Rightarrow \dfrac{{\sqrt 3 }}{1} = \dfrac{{3000\sqrt 3 }}{{AB}}{\text{ }}\left[ {\because \tan \left( {{{60}^0}} \right) = \sqrt 3 } \right] \\
   \Rightarrow AB = 3000m \\
 $
Similarly,
$
  \therefore {\text{ In }}\Delta ACD,\tan \left( {\angle DAC} \right) = \dfrac{{DC}}{{AC}} \\
   \Rightarrow \tan \left( {{{30}^0}} \right) = \dfrac{h}{{AC}} \\
   \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{3000\sqrt 3 }}{{AC}}{\text{ }}\left[ {\because \tan \left( {{{30}^0}} \right) = \dfrac{1}{{\sqrt 3 }}} \right] \\
   \Rightarrow AC = \left( {3000\sqrt 3 \times \sqrt 3 } \right)m \\
   \Rightarrow AC = 9000m \\
 $
Now the distance travelled by the aeroplane according to the figure is $BC$ .
$
   \Rightarrow BC = AC - AB \\
   \Rightarrow BC = 9000m - 3000m \\
   \Rightarrow BC = 6000m \\
   \Rightarrow BC = 6km{\text{ }}\left[ {\because 1000m = 1km} \right] \\
 $
Therefore, the plane covers $6km$ in $30$ seconds.
So the speed of the plane is
$
  {\text{speed = }}\dfrac{{{\text{distance}}}}{{{\text{time}}}} \\
   \Rightarrow {\text{speed}} = \dfrac{{6000m}}{{30{\text{second}}}} \\
   \Rightarrow {\text{speed}} = 200\dfrac{m}{{\sec }} \\
 $
Hence, the speed of the aeroplane is $200\dfrac{m}{{\sec }}$ .

Note- In order to solve such questions of height and distances, figures are a must to start the solution and also for better understanding. Trigonometric values at some particular angles such as ${30^0},{60^0},{90^0}....$ must be remembered. Also take special care of units at the time of finding speed of some moving object.