Question

The angle of elevation of a cloud from a point ‘h’ metres above a lake is $\alpha $ and the angle of depression of its reflection in the lake is $\beta $. Prove that the distance of the cloud from the point of observation is $\dfrac{2h\sec \alpha }{\tan \beta -\tan \alpha }$.

Answer 1

Hint: Assume that the distance of the cloud from the point of observation is ‘d’. Draw a rough diagram of the given conditions and then use the formula $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$ and $\sec \theta =\dfrac{\text{hypotenuse}}{\text{base}}$ in different right angle triangles and substitute the given values to get the distance.

Complete step by step answer:

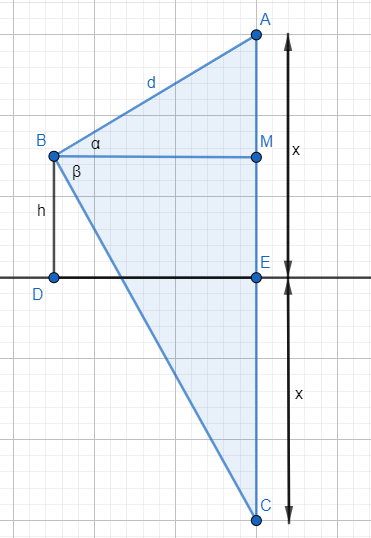
According to the above figure:
Let A be the cloud and the observer is at point B which is ‘h’ metres above the lake level. Let the reflection of the cloud below the lake level is at point C. Point D and E are at lake level.
We have assumed the height of the cloud above the lake level as ‘x’. Therefore, AE = x. Also, assume that the distance BM is ‘y’.
Now, in right angle triangle ABM,
$\angle ABM=\alpha $
We know that, $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$. Therefore,
$\tan \alpha=\dfrac{AM}{BM}$
Since, BD = ME = h, because they are opposite sides of the rectangle BDEM. Therefore,
AM = AE – EM = x – h.
$\begin{align}
  & \Rightarrow \tan \alpha =\dfrac{AM}{BM} \\
 & \Rightarrow \tan \alpha =\dfrac{x-h}{y} \\
 & \Rightarrow y=\dfrac{x-h}{\tan \alpha }.......................(i) \\
\end{align}$
Now, we know that, $\sec \theta =\dfrac{\text{hypotenuse}}{\text{base}}$. Therefore,
\[\begin{align}
  & \sec \alpha =\dfrac{AB}{BM} \\
 & \Rightarrow \sec \alpha =\dfrac{d}{y} \\
 & \Rightarrow y=\dfrac{d}{\sec \alpha }.....................(ii) \\
\end{align}\]
Substituting the value of y from equation (ii) in equation (i), we get,
$\dfrac{d}{\sec \alpha }=\dfrac{x-h}{\tan \alpha }...................(iii)$
Now, in right angle triangle BMC,
\[\angle CBM=\beta \]
We know that, $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$. Therefore,
$\tan \beta =\dfrac{CM}{BM}$
We know that, from the laws of angle of reflection we have, the distance of the object and its image formed by the plane mirror are equal. Therefore, considering the lake as the plane mirror, we have,
AE = CE = x.
CM = CE + ME = h + x
\[\begin{align}
  & \Rightarrow \tan \beta =\dfrac{h+x}{y} \\
 & \Rightarrow y=\dfrac{h+x}{\tan \beta } \\
 & \Rightarrow \dfrac{d}{\sec \alpha }=\dfrac{h+x}{\tan \beta } \\
 & \Rightarrow \dfrac{d\tan \beta }{\sec \alpha }=h+x \\
 & \Rightarrow x=\dfrac{d\tan \beta }{\sec \alpha }-h.........................(iv) \\
\end{align}\]
Substituting the value of x from equation (iv) in equation (iii), we get,
$\begin{align}
  & \dfrac{d}{\sec \alpha }=\dfrac{\dfrac{d\tan \beta }{\sec \alpha }-h-h}{\tan \alpha } \\
 & \Rightarrow \dfrac{d}{\sec \alpha }=\dfrac{\dfrac{d\tan \beta }{\sec \alpha }-2h}{\tan \alpha } \\
\end{align}$
By cross-multiplication we get,
$\begin{align}
  & d\tan \alpha =d\tan \beta -2h\sec \alpha \\
 & \Rightarrow d\tan \beta -d\tan \alpha =2h\sec \alpha \\
 & \Rightarrow d(\tan \beta -\tan \alpha )=2h\sec \alpha \\
 & \Rightarrow d=\dfrac{2h\sec \alpha }{(\tan \beta -\tan \alpha )} \\
\end{align}$

Note: One may get confused in removing the unknown variables. Therefore, remember that we have to find the value of variable ‘d’ and we have to remove all other variables. We have used the tangent and secant of the given angle because the required distance, that needs to be proved, is expressed in the form of these functions.