Question

The angle between the two hands of a clock at 4:30 p.m. is $\underline{\text{ }}.$
A. $45{}^\circ $
B. $90{}^\circ $
C. $180{}^\circ $
D. $60{}^\circ $

Answer 1

Hint: We solve this question by using basic concepts of angles. We use the concept that a clock is circular so it has a total angle of $360{}^\circ .$ Using this, we calculate the distance or amount by which the hour and minute hands move in order to cover a certain length on the clock. Then by observing the position of the two hands of a clock at 4:30 p.m. we determine the angle between them.

Complete step by step answer:
In order to solve this question, let us first draw the position of the hands of the clock at the given time.

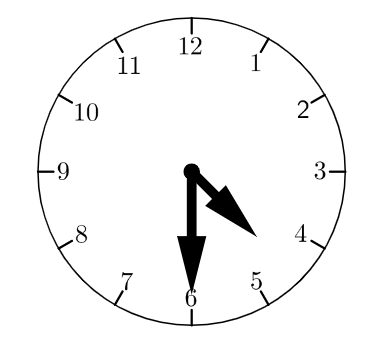
This is shown in the figure above, the time depicted here is 4:30. This is the same for a.m. or p.m. because clocks work on the 12-hour format.
Now, let us consider the hour hand. When it moves a full circle, we can say that it covers a total of $360{}^\circ .$ This means that to find out the number of degrees it moves in 1 hour, we can divide the total $360{}^\circ $ by 12 hours.
$\Rightarrow \dfrac{360{}^\circ }{12}=30{}^\circ $
Hence, the hour hand moves $30{}^\circ $ in 1 hour.
Similarly, let us find the minute hand now. When it moves a full circle, we can say that it covers a total of $360{}^\circ .$ This means that to find out the number of degrees it moves in 1 minute, we can divide the total $360{}^\circ $ by 60 minutes.
$\Rightarrow \dfrac{360{}^\circ }{60}=6{}^\circ $
Hence, the hour hand moves $6{}^\circ $ in 1 minute.
We also need to find out the amount by which the hour hand moves for each minute. This can be found by dividing the total number of degrees divided by the total number of minutes in 12 hours which is 12 multiplied by 60.
$\Rightarrow \dfrac{360{}^\circ }{12\times 60}=0.5{}^\circ $
Hence, the hour hand moves $0.5{}^\circ $ for every minute.
Now, the time is 4:30. This means that the hour hand, starting from 12, moves by a total angle given by,
$\Rightarrow 4\times 30{}^\circ +30\times 0.5{}^\circ $
Multiplying the terms,
$\Rightarrow 120{}^\circ +15{}^\circ $
Adding the two terms,
$\Rightarrow 135{}^\circ $
Now the minute hand moves by 30 minutes which is represented as,
$\Rightarrow 30\times 6{}^\circ $
Multiplying the two, we get
$\Rightarrow 180{}^\circ $
Now to find the angle between the two hands of the clock, we simply subtract the two angles obtained.
$\Rightarrow 180{}^\circ -135{}^\circ =45{}^\circ $
Hence, the angle between the two hands of a clock at 4:30 p.m. is $45{}^\circ .$

So, the correct answer is “Option A”.

Note: We need to know how to compute angles for the hands moving in the clock. An important point to note here is that the hour hand not only moves when the hours change but it also moves due to the change in minutes of the clock. That is why we have an additional 30 terms in the angles covered by the hour hand.