Question

The altitudes of the triangle are 12,15 and 20 units. The largest angle in the triangle is:
A. \[{75^0}\]
B. \[{90^0}\]
C. \[{120^0}\]
D. \[{135^0}\]

Answer 1

Hint: First of all, consider a triangle \[\Delta ABC\] with side lengths \[a,b,c\] units. Then draw the figure of the considered triangle with the given altitudes. Further, equate the areas of the triangle with all the altitudes by using the formula of area of the triangle with altitude and its base. Then prove the considered triangle as a right-angle triangle by using the Pythagoras theorem. So, use this concept to reach the solution to the given problem.
Let us consider a \[\Delta ABC\] with side lengths \[a,b,c\] units.

Complete step-by-step solution:
Given that the altitudes of the \[\Delta ABC\] are 12,15 and 20 units as shown in the below figure:

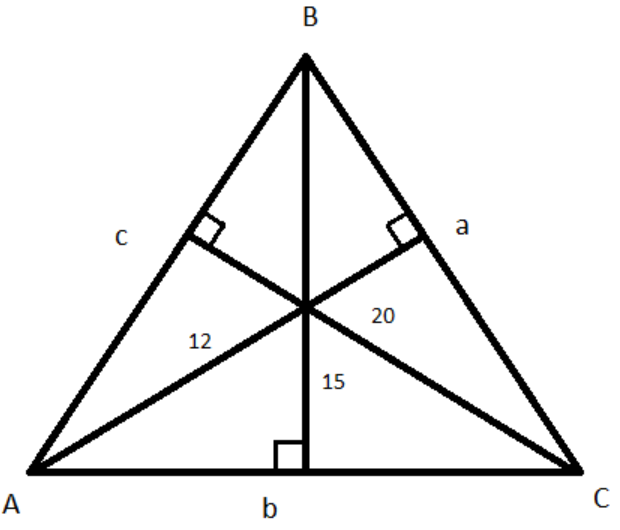
We know that if \[h\] is the height of the triangle and \[x\] is the length of base of the triangle then the area of that triangle is given by \[\dfrac{1}{2} \times x \times h\].
So, area of \[\Delta ABC\] \[ = \dfrac{1}{2} \times a \times 12 = \dfrac{1}{2} \times b \times 15 = \dfrac{1}{2} \times c \times 20\]
Let \[\dfrac{1}{2} \times a \times 12 = \dfrac{1}{2} \times b \times 15 = \dfrac{1}{2} \times c \times 20 = k\]
Taking first and last term we have
\[ \Rightarrow \dfrac{1}{2} \times a \times 12 = k \\
  \therefore a = \dfrac{{2k}}{{12}} = \dfrac{{2k}}{{12}} \times \dfrac{5}{5} = \dfrac{{10k}}{{60}} \]
Taking the second and last term we have
\[ \Rightarrow \dfrac{1}{2} \times b \times 15 = k \\
  \therefore b = \dfrac{{2k}}{{15}} = \dfrac{{2k}}{{15}} \times \dfrac{4}{4} = \dfrac{{8k}}{{60}} \]
Taking the third and the last term we have
\[ \Rightarrow \dfrac{1}{2} \times c \times 20 = k \\
  \therefore c = \dfrac{{2k}}{{20}} = \dfrac{{2k}}{{20}} \times \dfrac{3}{3} = \dfrac{{6k}}{{60}} \]
Let us consider \[{b^2} + {c^2}\]
\[ \Rightarrow {b^2} + {c^2} = {\left( {\dfrac{{8k}}{{60}}} \right)^2} + {\left( {\dfrac{{6k}}{{60}}} \right)^2} \\
   \Rightarrow {b^2} + {c^2} = \dfrac{{64{k^2}}}{{3600}} + \dfrac{{36{k^2}}}{{3600}} \\
  \therefore {b^2} + {c^2} = \dfrac{{100{k^2}}}{{3600}}...............................\left( 1 \right) \]
And consider the value of \[{a^2}\]
\[ \Rightarrow {a^2} = {\left( {\dfrac{{10k}}{{60}}} \right)^2} \\
  \therefore {a^2} = \dfrac{{100{k^2}}}{{3600}}...................................\left( 2 \right) \]
From equation (1) and (2), we have
\[{b^2} + {c^2} = {a^2}\]
We know that Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides” i.e., \[{\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Adjacent side}}} \right)^2} + {\left( {{\text{Opposite side}}} \right)^2}\].
So, clearly the \[\Delta ABC\] with sides \[a,b,c\] forms a right-angle triangle and it can be redrawn as:

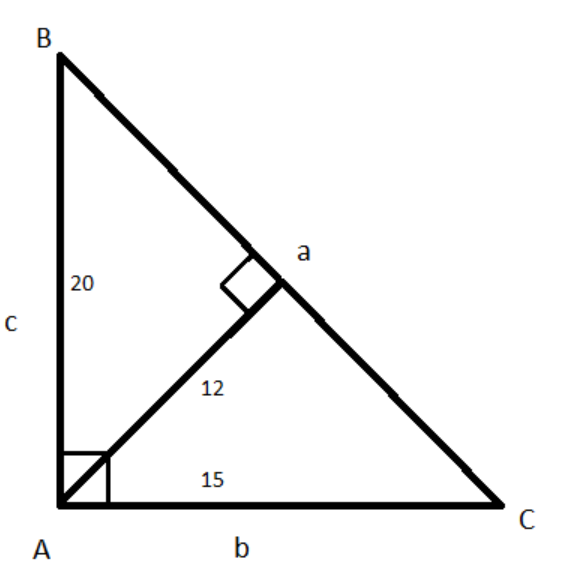
We know that in a right-angle triangle the greatest angle is \[{90^0}\].
Thus, the greatest angle in \[\Delta ABC\] is \[{90^0}\].

Hence, the correct option is B. \[{90^0}\]

Note: After redrawing the triangle \[\Delta ABC\], we can observe that at point A it is the right angle and the values of sides \[b,c\] are 15,20 units respectively. The third side \[a\] can be found by Pythagoras theorem i.e., \[a = \sqrt {{{\left( {15} \right)}^2} + {{\left( {20} \right)}^2}} = \sqrt {225 + 400} = \sqrt {625} = 25\].